Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T12:33:19.814Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of the spaces Cm(Ω) ∩ Hk, p (Ω)

Published online by Cambridge University Press:  24 October 2008

A. A. Albanese ,
G. Metafune  and
V. B. Moscatelli
A. A. Albanese
Affiliation:
Dipartimento di Matematica, Università, C.P. 193, 73100 Lecce, Italy
G. Metafune
Affiliation:
Dipartimento di Matematica, Università, C.P. 193, 73100 Lecce, Italy
V. B. Moscatelli
Affiliation:
Dipartimento di Matematica, Università, C.P. 193, 73100 Lecce, Italy
Get access Rights & Permissions [Opens in a new window]

Extract

The present work has its motivation in the papers [2] and [6] on distinguished Fréchet function spaces. Recall that a Fréchet space E is distinguished if it is the projective limit of a sequence of Banach spaces En such that the strong dual E′β is the inductive limit of the sequence of the duals E′n. Clearly, the property of being distinguished is inherited by complemented subspaces and in [6] Taskinen proved that the Fréchet function space C(R) ∩ L1(R) (intersection topology) is not distinguished, by showing that it contains a complemented subspace of Moscatelli type (see Section 1) that is not distinguished. Because of the criterion in [1], it is easy to decide when a Frechet space of Moscatelli type is distinguished. Using this, in [2], Bonet and Taskinen obtained that the spaces 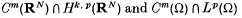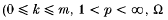open in RN) are distinguished, by proving that they are isomorphic to complemented subspaces of distinguished Fréchet spaces of Moscatelli type.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 3 , October 1996 , pp. 489 - 498
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bonet, J. and Dierolf, S.. Fréchet spaces of Moscatelli type. Rev. Mat. Univ. Complut. Madrid 2 (suppl.) (1989), 77–92.Google Scholar
[2]Bonet, J. and Taskinen, J.. Non-distinguished Fréchet function spaces. Bull. Soc. Roy. Sci. Liège 58 (1989), 483–490.Google Scholar
[3]Ciesielski, Z. and Domsta, J.. Construction of an orthonormal basis in C m(I d) and . Studia Math. 41 (1972), 211–224.CrossRefGoogle Scholar
[4]Mattila, P. and Taskinen, J.. Remarks on bases in a Frechet function space. Rev. Mat. Univ. Complut. Madrid 6 (1993), 83–99.Google Scholar
[5]Moscatelli, V. B.. Fréchet spaces without continuous norms and without bases. Bull. London Math. Soc. 12 (1980), 63–66.CrossRefGoogle Scholar
[6]Taskinen, J.. Examples of non-distinguished Fréchet spaces. Ann. Acad. Sci. Fenn. Ser A J Math. 14 (1989), 75–88.Google Scholar