The potential of a circular current
Published online by Cambridge University Press: 24 October 2008
Extract
The 3-dimensional potential due to a charged circle can be derived in various ways which lead to the same expression in terms of the toroidal coordinate σ through Legendre functions of s (= cosh σ). Applying the same methods to the magnetic potential of a circular current we find various results: (a) Legendre's equation yields no solution (§4·1). (b) The appropriate transformation from cylindrical to toroidal coordinates gives a Fourier series (equation (48)) the coefficients 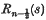 of which, though not Legendre functions, are related to them by the identity (§4·2)
of which, though not Legendre functions, are related to them by the identity (§4·2) 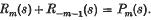 By this method we also derive expressions in elliptic integrals (equations (56), (58)). (c) Direct integration of the solid angle gives an alternative expression in elliptic integrals (equation (59)).
By this method we also derive expressions in elliptic integrals (equations (56), (58)). (c) Direct integration of the solid angle gives an alternative expression in elliptic integrals (equation (59)).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 2 , April 1961 , pp. 385 - 392
- Copyright
- Copyright © Cambridge Philosophical Society 1961
References
REFERENCES
- 3
- Cited by


