The conformal tensors of a Riemannian space Vn are classified and analysed, mainly in terms of the ‘conformal number’ χ which is defined as a certain linear combination of the numbers that characterize the transformation modes of a conformal tensor. In the case of zero rest mass fields (5), χ – 1 is just the spin. Conformal concomitants of the metric tensor and its derivatives up to a finite order m are considered and, in particular, those tensors which are polynomials in the 2nd and higher derivatives of the metric tensor (called conformal P-tensors of order m). The algebraic structure of such a tensor is described by a set of m − 1 integers (S2, …, Sm), referred to as the structure of F and defined in an invariant way in terms of the various polynomial degrees of F and its partial derivatives. The structure of F is related to the m transformation modes of F by the formula: 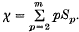. Thus for P-tensors, χ = 0, 2, 3, … and m ≤ χ. The set of structures (S2, …, Sm) of all conformal P-tensors of order less than or equal to m, forms an Abelian monoid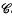 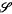m, with addition defined componentwise. In a general V4, it is found that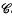 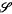4 consists of all triplets (S2, S3, S4) ∈ 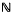3 for which S3 ≤ 4S2. Finally, new conformal P-tensors are constructed so that examples can be given corresponding to every structure in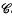 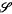4. One also obtains, for each value of χ, a general formula which expresses any conformal P-tensor with conformal number χ in terms of a standard sequence of conformal P-tensors.