Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T04:53:31.506Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Stability Problem in Hydrodynamics

Published online by Cambridge University Press:  24 October 2008

Chaim L. Pekeris
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper deals with the problem of the effect of two-dimensional first order disturbances on the linear and parabolic flows of a viscous fluid. If the laminar flow is in the direction x and is bounded by the planes y = ±h, and if the stream function of the disturbance is assumed to be of the form 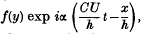, it is found that, for small Reynolds numbers R (= Uh/v), C can be developed in the power series

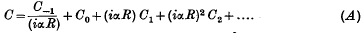
The first term in (1) corresponds to a disturbance in still water and is known from Rayleigh's investigation of that problem; the succeeding C's are real and can be obtained by an application of Schrödinger's perturbation theory of wave mechanics. In the case of the parabolic flow, expressions for C0 and C1 were thus derived for both the symmetrical and anti-symmetrical types of disturbance.

The imaginary part of C, as represented by 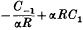in this approximation, is found to be positive. When α is of the order of unity, the value of R which makes the second term of the first is about 50 for the symmetrical disturbance and 100 for the antisymmetrical disturbance. C0, the first term in the expression for the phase velocity, is less than 1 and increases with α, which implies a group velocity greater than the phase velocity.

In the case of the linear flow it is found that the C's with even subscripts vanish, implying a vanishing phase velocity. This verifies the assumption to that effect made by Southwell and Chitty, and it also suggests that the region of convergence of (A) is limited to the range of values of R covered by these authors. Expressions are derived for C1 and C3 and are evaluated for α=1. The formulae thus obtained for the damping constant give an initial decrease with R, which is not shown in the corresponding curve of Southwell and Chitty.

An alternative method of determining C is outlined in the last section. Use is made of the orthogonal system of the characteristic functions for the vorticity of a disturbance in still water. The equation determining C is reduced to an infinite determinant in which C occurs only in the diagonal elements. When R→0, the determinant can be evaluated and the roots C are found to coincide with the first two terms in (A).

Finally it is shown that the two-dimensional laminar flow is stable for values of R less than the smaller of the quantities 2α and α3.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 1 , January 1936 , pp. 55 - 66
Copyright
Copyright © Cambridge Philosophical Society 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* For a review of the literature on the subject see Lamb, , Hydrodynamics (1932), 670Google Scholar, also ref. §, p. 2.

* Taylor, G. I., Phil. Trans. A, 223 (1923), 289.CrossRefGoogle Scholar

† Hopf, L., Ann. d. Physik, 44 (1914), 1.CrossRefGoogle Scholar

‡ Mises, v., Jahresb. d.D. Math. Ver. 21 (1912), 241.Google Scholar

§ Southwell, R. V. and Chitty, L., Phil. Trans. A, 229 (1930), 205.CrossRefGoogle Scholar

∥ Rayleigh, , Scientific Papers, Vol. 3, p. 582.Google Scholar

Schrödinger, E., Ann. d. Physik, 80 (1926), 437.CrossRefGoogle Scholar See also Sommerfeld, A., Ergänzungsband (1929), 172.Google Scholar

* In the latter case the laminar velocity is assumed to be given by yU/h, where y ranges from − 1 to 1.

* It can easily be shown that a disturbance which is independent of x (α=0) is damped.

† Rayleigh, , Scientific Papers, Vol. 3, p. 582.Google Scholar

* Goldstein, S., Proc. Camb. Phil. Soc. 32 (1936), 40–54.CrossRefGoogle Scholar I am indebted to Dr Goldstein for having shown me his unpublished results and for the opportunity to discuss the subject matter with him.

* For a given state of laminar flow Southwell and Chitty assign a Reynolds number which is four times the value of R in (2.4) and (2.5).

* Fourier, J., Analytical theory of heat (translated by A. Freeman, 1878), pp. 268, 441.Google Scholar

† Fujisawa, R., Journ. Coll. Sci. Imp. Univ. Japan, 2 (1889), 1Google Scholar; Ford, W. B., Studies in divergent series and summability (1916), p. 142.Google Scholar

‡ This solves the problem discussed by Synge, J. L., Proc. Lond. Math. Soc. (2), 40 (1935), 23.Google Scholar

* The asymmetry in the determinant can be traced to the fact that equation (7) is not self-adjoint.

† The stability of the linear flow for disturbances of vanishing wavelength (α→∞) was proved by Rayleigh, , Scientific Papers, Vol. 6, p. 347.Google Scholar