Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T13:24:53.182Z Has data issue: false hasContentIssue false
  • English
  • Français

On the solution of certain integral equations by generalized functions

Published online by Cambridge University Press:  24 October 2008

J. B. Miller
J. B. Miller
Affiliation:
Australian National UniversityCanberra
Get access Rights & Permissions [Opens in a new window]

Extract

This note is concerned with a method by which generalized solutions can be shown to exist for certain types of integral equations

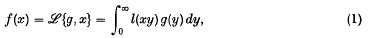
where f(x) ∈ L2(0, ∞). The method is briefly this. An extended meaning is given to such equations by using generalized functions of a particular type. Then, if (1) denotes a transformation which has no everywhere-defined inverse in the usual sense, it may be possible to define in the extended sense an inverse transformation

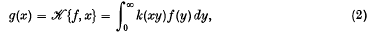
so that if f is given, a generalized function g = 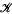can be determined as a solution of (1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 4 , October 1961 , pp. 767 - 777
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Miller, J. B., Hilbert spaces of generalized functions extending L 2, (I). J. Australian Math. Soc. 1 (1960), 281–98.CrossRefGoogle Scholar
(2)Titchmarsh, E. C., Introduction to the theory of Fourier integrals, 2nd ed. (Oxford, 1948).Google Scholar
(3)Bateman Manuscript Project. Tables of integral transforms (McGraw-Hill, 1954).Google Scholar