Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T14:39:17.816Z Has data issue: false hasContentIssue false
  • English
  • Français

On the numerical solution of a class of partial differential equations

Published online by Cambridge University Press:  24 October 2008

A. S. Douglas
A. S. Douglas
Affiliation:
Mathematical Laboratory, Cambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

For a suitable choice of E*, the solution as t becomes large of the equation

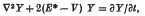
where Y is given independent of t over the space boundaries, tends to the ground state solution of the wave equation

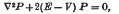
with the same boundary conditions on P as on Y. As a preliminary to using this relation to solve wave equations in more than one variable, the solution of the equation

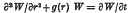
has been studied. Methods of numerical solution are discussed, and the convergence of these is examined. Some practical experiments using an electronic computing machine are described.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 54 , Issue 2 , April 1958 , pp. 214 - 218
Copyright
Copyright © Cambridge Philosophical Society 1958

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Boys, S. F.Proc. Roy. Soc. A, 200 (1950), 542.Google Scholar
(2)Hartree, D. R. Private communication.Google Scholar
(3)O'Brien, G. G., Hyman, M. A. and Kaplan, S. A.J. Math. Phys. 29 (1951), 223.CrossRefGoogle Scholar
(4)Crank, J. and Nicholson, M.Proc. Camb. Phil. Soc. 43 (1947), 50.CrossRefGoogle Scholar
(5)Frankel, S. P. and Du Fort, E. C.M.T.A.C. 7 (1953), 135.Google Scholar
(6)Juncosa, M. L. and Young, D. M.Proc. Camb. Phil. Soc. 53 (1957), 448.CrossRefGoogle Scholar
(7)Peaceman, D. W. and Rachford, H. H.J. Soc. Industr. Appl. Math. 3 (1955), 28.CrossRefGoogle Scholar
(8)Douglas, J.J. Soc. Industr. Appl. Math. 3 (1955), 42.CrossRefGoogle Scholar
(9)Crandall, S. H.Quart. Appl. Math. 13 (1955), 318.CrossRefGoogle Scholar
(10)Richardson, L. F.Phil. Trans. A, 242 (1950), 439.Google Scholar
(11)Kemble, E. C.The fundamental principles of quantum mechanics (New York, 1937).Google Scholar
(12)Phelps, J. Thesis (Cambridge, 1956).Google Scholar