Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zimmermann, Bruno P.
2010.
On minimal actions of finite simple groups on homology spheres and Euclidean spaces.
Rendiconti del Circolo Matematico di Palermo,
Vol. 59,
Issue. 3,
p.
451.
Mundet i Riera, Ignasi
2019.
Finite group actions on homology spheres and manifolds with nonzero Euler characteristic.
Journal of Topology,
Vol. 12,
Issue. 3,
p.
744.


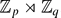 , for primes
, for primes 