Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T14:25:12.409Z Has data issue: false hasContentIssue false
  • English
  • Français

On the continuity of the P.S.-function

Published online by Cambridge University Press:  24 October 2008

M. McCrudden
M. McCrudden
Affiliation:
University of Washington, Seattle, Washington 98105, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a locally compact, unimodular, topological group with μ Haar measure on G, and μ* the corresponding inner measure. If 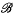(G) denotes the Borel subsets of G of finite measure, and V(G) = {μ(E):E∈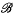(G)}, then the Product Set function, or P.S.-function, of the group G, written ΦG, is defined by

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 2 , September 1970 , pp. 359 - 361
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Henstock, R. and Macbeath, A. M.On the measure of sum-sets, 1. Proc. London Math. Soc. 3 (1953), 182–194.CrossRefGoogle Scholar
(2)Macbeath, A. M.On the measure of product sets in a topological group. J. London Math. Soc. 35 (1960), 403–407.CrossRefGoogle Scholar
(3)McCrudden, M.On product sets in a unimodular group. Proc. Cambridge Philos. Soc. 64 (1968), 1001–1007.CrossRefGoogle Scholar
(4)Weil, A.L'integration dans les groupes lopologiques et ses applications (Paris, 1953).Google Scholar