Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T14:41:09.060Z Has data issue: false hasContentIssue false
  • English
  • Français

On the computation of oscillatory integrals

Published online by Cambridge University Press:  24 October 2008

Yudell L. Luke
Yudell L. Luke
Affiliation:
Midwest Research Institute Kansas City, Missouri
Get access Rights & Permissions [Opens in a new window]

Extract

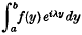Computation of integrals of the type is of frequent occurrence in applied problems. Here λ is real and i is the imaginary unit. Tables of the integrals are often required for a wide range of λ values, some of which may be quite large. Tabulation of the integrand for each λ, followed by ordinary methods of numerical integration, is slow and tedious because the number of points required increases with increasing λ. In this paper formulas are given so that once f(y) is tabulated over the range of interest, the integral in question can be easily evaluated for any λ.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 2 , April 1954 , pp. 269 - 277
Copyright
Copyright © Cambridge Philosophical Society 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Beard, R. E.Some notes on approximate product integration. J. Inst. Actu. 73 (1948), 356–414.CrossRefGoogle Scholar
(2)Filon, L. N. G.On a quadrature formula for trigonometric integrals. Proc. roy. Soc. Edinb. 49 (1929), 38–47.CrossRefGoogle Scholar
(3)Harvard University Computation Laboratory. Tables of the function sin Φ/Φ and of its first eleven derivatives (Harvard, 1949).Google Scholar
(4)Milne, W. E.The remainder in linear methods of approximation. J. Res. Bur. Stand. 43 (1949), 501–11.CrossRefGoogle Scholar
(5)Milne, W. E.Numerical calculus (Princeton, 1949), pp. 108–16.CrossRefGoogle Scholar
(6)National Bureau of Standards. Struve function of order three-halves. J. Res. 50 (1953), 21–9.Google Scholar
(7)Nikolaeva, M. V.On approximate evaluation of oscillating integrals (in Russian). Trav. Inst. math. Stekloff, 28 (1949), 26–32.Google Scholar
(8)Sheldon, J. W. Numerical evaluation of integrals of the form . International Business Machines Corporation Seminar (New York, 1950), pp. 74–8.Google Scholar