Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T19:48:33.917Z Has data issue: false hasContentIssue false
  • English
  • Français

On the absolute Hausdorff summability factors of a Fourier series

Published online by Cambridge University Press:  24 October 2008

N. Tripathy
N. Tripathy
Affiliation:
Ravenshaw College, Cuttack, India
Get access Rights & Permissions [Opens in a new window]

Extract

Let 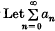be a given infinite series with the sequence of partial sums {sn}. Then the sequence-to-sequence Hausdorff transformation of the sequence {sn} is given by

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 2 , September 1969 , pp. 355 - 363
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bosanquet, L. S.The absolute Cesàro summability of a Fourier Series. Proc. Lond. Math. Soc. 41 (1936), 517–529.Google Scholar
(2)Cheng, M. T.Summability factors of Fourier Series. Duke Math. J. 15 (1948), 17–27.Google Scholar
(3)Hardy, G. H.Divergent series (Oxford, 1949).Google Scholar
(4)Hausdorff, F.Summationsmethoden und momentfolgen I. Math. Z. 9 (1921), 74–109.Google Scholar
(5)Knopp, K. and Lorentz, G. G.Beitrage zur absoluten Limitierung. Arch. Math 2 (1949/1950), 10–16.Google Scholar
(6)Kuttner, B.On the ‘second theorem of consistency’ for Riesz summability (II). J. London Math Soc. 27 (1952), 207–217.CrossRefGoogle Scholar
(7)Ramanujan, M. S.On Hausdorff and quasi-Hausdorff methods of summability. Quart. J. Math. Oxford Ser. 8 (1957), 197–213.Google Scholar
(8)Tbipathy, N.On the absolute Hausdorff summability of Fourier series. J. London Math. Soc. 44 (1969), 15–25.CrossRefGoogle Scholar
(9)Zygmund, A.Trigonometric series (Cambridge, 1959).Google Scholar