Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T13:15:56.031Z Has data issue: false hasContentIssue false
  • English
  • Français

On some results involving generalized hypergeometric polynomials

Published online by Cambridge University Press:  24 October 2008

Manilal Shah
Manilal Shah
Affiliation:
Department of Mathematics, P.M.B.G. College, Indore (M.P.), India
Get access Rights & Permissions [Opens in a new window]

Extract

The generalized hypergeometric polynomial ((7), equation (2·1)) has been defined by

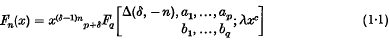
where the symbol Δ(δ, −n) represents the set of δ-parameters:

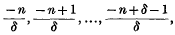
and δ, n are positive integers. The polynomial is in a generalized form which yields many known polynomials on specializing the parameters.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 1 , January 1969 , pp. 87 - 92
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Fasenmyer, Sister M. Celine. Some generalized hypergeometric polynomials. Bull. Amer. Math. Soc. 53 (1947), 806–812.CrossRefGoogle Scholar
(2)Khandekar, P. R.On a generalization of Rice's polynomial. 1. Proc. Nat. Acad. Sci., India Part A, 34 (1964), 157–162.Google Scholar
(3)MacRobert, T. M.Infinite series of E-functions. Math. Z. 71 (1959), 143–145.CrossRefGoogle Scholar
(4)MacRobert, T. M.Fourier Series for E-functions. Math. Z. 75 (1961), 79–82.CrossRefGoogle Scholar
(5)Rice, S. O.Some properties of Duke Math. J. 6 (1960), 108–119.Google Scholar
(6)Rainville, E. D.Special functions (New York, 1960).Google Scholar
(7)Shah, Manilal. Certain integrals involving the product of two generalized hypergeometric polynomials. Proc. Nat. Acad. Sci., India Part A, 37 (1967), 79–96.Google Scholar