Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Çinlar, Erhan
1969.
Markov renewal theory.
Advances in Applied Probability,
Vol. 1,
Issue. 2,
p.
123.
�inlar, E.
and
Pinsky, M.
1971.
A stochastic integral in storage theory.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 17,
Issue. 3,
p.
227.
Arjas, E.
1972.
On a fundamental identity in the theory of semi-Markov processes.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
258.
Arjas, E.
1972.
On a fundamental identity in the theory of semi-Markov processes.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
258.
Iosifescu, M.
and
Tăutu, P.
1973.
Stochastic processes and applications in biology and medicine I.
Vol. 3,
Issue. ,
p.
163.
Çinlar, Erhan
1974.
Periodicity in Markov renewal theory.
Advances in Applied Probability,
Vol. 6,
Issue. 1,
p.
61.
Çinlar, Erhan
1974.
Periodicity in Markov renewal theory.
Advances in Applied Probability,
Vol. 6,
Issue. 1,
p.
61.
Disney, Ralph L.
and
Cherry, W. Peter
1974.
Mathematical Methods in Queueing Theory.
Vol. 98,
Issue. ,
p.
23.
Cherenkov, A. P.
1974.
Existence theorems for a semi-Markov process with an arbitrary set of states.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 15,
Issue. 4,
p.
367.
Kovalenko, I. N.
1974.
Queueing theory.
Journal of Soviet Mathematics,
Vol. 2,
Issue. 1,
p.
1.
Cherenkov, A. P.
1975.
Additive functionals of regular semi-Markov processes.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 18,
Issue. 4,
p.
957.
Korolyuk, V. S.
Brodi, S. M.
and
Turbin, A. F.
1975.
Semi-markov processes and their applications.
Journal of Soviet Mathematics,
Vol. 4,
Issue. 3,
p.
244.
Karr, Alan F.
1975.
Weak convergence of a sequence of Markov chains.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 33,
Issue. 1,
p.
41.
Cherenkov, A. P.
1975.
Additive functionals of semi-Markov processes with absorption.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 17,
Issue. 2,
p.
189.
Feldman, Richard M.
1976.
Optimal replacement with semi-Markov shock models.
Journal of Applied Probability,
Vol. 13,
Issue. 1,
p.
108.
Korolyuk, V. S.
and
Turbin, A. F.
1976.
Proceedings of the Third Japan — USSR Symposium on Probability Theory.
Vol. 550,
Issue. ,
p.
297.
Feldman, Richard M.
1976.
Optimal replacement with semi-Markov shock models.
Journal of Applied Probability,
Vol. 13,
Issue. 1,
p.
108.
Jacobs, P. A.
and
Lewis, P. A. W.
1977.
A mixed autoregressive-moving average exponential sequence and point process (EARMA 1,1).
Advances in Applied Probability,
Vol. 9,
Issue. 1,
p.
87.
Nummelin, Esa
1977.
On the concepts of α-recurrence and α-transience for Markov renewal process.
Stochastic Processes and their Applications,
Vol. 5,
Issue. 1,
p.
1.
FELDMAN, RICHARD M.
1977.
The Theory and Applications of Reliability with Emphasis on Bayesian and Nonparametric Methods.
p.
215.


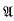 a σ-algebra of subsets of
a σ-algebra of subsets of
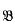 the Borel sets of
the Borel sets of