Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T14:21:37.552Z Has data issue: false hasContentIssue false
  • English
  • Français

On hearing the shape of a drum: further results

Published online by Cambridge University Press:  24 October 2008

K. Stewartson  and
R. T. Waechter
K. Stewartson
Affiliation:
Department of Mathematics, University College London
R. T. Waechter
Affiliation:
Department of Mathematics, University College London
Get access Rights & Permissions [Opens in a new window]

Extract

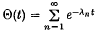1. Introduction. The underlying problem is to deduce the shape of a drum or plane uniform membrane from the knowledge of its spectrum of eigenvalues ωn = i√λn. It has been shown by Kac(3) that some progress is possible on establishing the leading terms of the asymptotic expansion of the trace function for small positive t. In particular, for a simply connected membrane Ω bounded by a smooth convex curve Γ for which the displacement satisfies the wave equation ∇2ø = ∂2ø/∂t2 and Dirichlet conditions on Γ

where |Ω| = area of Ω, L = length of Γ, and the constant ⅙ is determined (apart from a factor) on integrating the curvature of the boundary; moreover, if Ω is permitted to have a finite number of smooth convex holes then the constant becomes ⅙(1–r), where r = number of holes.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 69 , Issue 2 , March 1971 , pp. 353 - 363
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Akhiezer, N. I.The classical moment problem (Oliver and Boyd, 1965).Google Scholar
(2)Fisher, M. E. J.Combinatorial Theory 1 (1966), 105–125.CrossRefGoogle Scholar
(3)Kac, M.Amer. Math. Monthly 73 (1966), no. 4, part II, 1–23.CrossRefGoogle Scholar
(4)Krein, M. G.Dokl. Akad. Nauk, SSSR 76 (1951), 345–348.Google Scholar
(5)McKean, J. P. and Singer, I. M. J.Differential Geom. 1 (1967), 43–69.Google Scholar
(6)Olver, F. W. J.Philos. Trans. Roy. Soc. London, Ser. A 247 (1954), 328–368.Google Scholar
(7)Pleijel, A.Ark. Mat. 2 (1954), 553–569.CrossRefGoogle Scholar