No CrossRef data available.
On diagonal values of probability vectors of infinitely many components
Published online by Cambridge University Press: 24 October 2008
Extract
Given † probability vector μ(X) = (μ1(X), … μk (X)) of a finite number of components on a Borel class of sets X, we say that μ(X0) has a diagonal value α if μi(X0) = α for all i = 1, 2,…,K. J. Neyman(l), (2), (3) has proved that in the class of Borel sets of real numbers any non-atomic vector μ(X) takes all diagonal values. A. Liapounoff has studied the full range of values of k-dimensional vector-valued measures and in two papers (4) he has proved that the range is closed and in the case of non-atomic measures the range is also convex. He also gave an example showing that neither of these results holds in the case of vectors of infinitely many components. A simplified proof of Liapounoff's results has been given by P. R. Halmos (5). In the present paper I study the range of values of probability vectors of infinitely many components. Various types of conditions are studied which are sufficient to imply that, for each ε > 0, 0 ≤ α ≤ 1, it is possible to find a set X such that
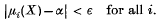
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 4 , October 1961 , pp. 759 - 766
- Copyright
- Copyright © Cambridge Philosophical Society 1961
References
REFERENCES
(1)Neyman, J. and Pearson, E. S., On the problem of the most efficient tests of statistical hypotheses. Philos. Trans. Roy. Soc. London, Ser. A, 231 (1933), 289–337.Google Scholar
(2)Neyman, J., Outline of a theory of statistical estimation based on the classical theory of probability. Philos. Trans. Roy. Soc. London, Ser. A, 236 (1937), 333–80.Google Scholar
(4)Liapounoff, A., Sur les fonctions-vecteurs completement additives. Izv. Akad. Nauk SSSR Ser. Mat. 4 (1940), 465–78, and 10 (1946), 277–9.Google Scholar
(5)Halmos, P. R., The range of a vector measure. Bull. American Math. Soc. 54 (1948), 416–21.CrossRefGoogle Scholar