Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T14:43:18.352Z Has data issue: false hasContentIssue false
  • English
  • Français

On derived functors of graded local cohomology modules

Published online by Cambridge University Press:  10 July 2018

TONY J. PUTHENPURAKAL  and
JYOTI SINGH
TONY J. PUTHENPURAKAL
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Mumbai 400076, India. e-mail: [email protected]
JYOTI SINGH
Affiliation:
Department of Mathematics, Visvesvaraya National Institute of Technology, Nagpur, 440010, India. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a field of characteristic zero and let R = K[X1, . . .,Xn], with standard grading. Let 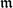${\mathfrak m}$ = (X1, . . ., Xn) and let E be the *injective hull of R/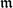${\mathfrak m}$. Let An(K) be the nth Weyl algebra over K. Let I, J be homogeneous ideals in R. Fix i, j ≥ 0 and set M = HiI(R) and N = HjJ(R) considered as left An(K)-modules. We show the following two results for which no analogous result is known in charactersitc p > 0.

  1. (i) 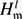$H^l_{\mathfrak m}$(TorRν(M, N)) ≅ E(n)al,ν for some al,ν ≥ 0.

  2. (ii) For all ν ≥ 0; the finite dimensional vector space TorAn(K)ν(M♯, N) is concentrated in degree -n (here M♯ is the standard right An(K)-module associated to M).

We also conjecture that for all i ≥ 0 the finite dimensional vector space ExtiAn(K)(M, N) is concentrated in degree zero. We give a few examples which support this conjecture.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 167 , Issue 3 , November 2019 , pp. 549 - 565
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Björk, J.-E. Rings of differential operators. North-Holland Math. Library 21 (North Holland, Amsterdam, 1979).Google Scholar
[2] Bruns, W. and Herzog, J. Cohen–Macaulay Rings. Camb. Stud. Adv. Math. 39 (Cambridge University Press, Cambridge, 1993).Google Scholar
[3] Lyubeznik, G. Finiteness properties of local cohomology modules (an application of D-modules to commutative algebra). Invent. Math. 113 (1993), no. 1, 41–55.Google Scholar
[4] Ma, L. and Zhang, W. Eulerian graded D-modules. Math. Res. Lett. 21 (2014), no. 1, 149–167.Google Scholar
[5] Puthenpurakal, T. J. de Rham cohomology of local cohomology modules, (English summary). Algebra App. (Springer Proc. Math. Stat. Springer, Singapore), 174 (2016), 159–181.Google Scholar
[6] Puthenpurakal, T. J. De Rham cohomology of local cohomology modules-the graded case. Nagoya Math. J. 217 (2015), 1–21.Google Scholar
[7] Walther, U. Algorithmic computation of local cohomology modules and the local cohomological dimension of algebraic varieties. Effective methods in algebraic geometry (Saint-Malo, 1998) J. Pure Appl. Algebra 139 (1999), 303–321.Google Scholar