Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-20T04:08:58.509Z Has data issue: false hasContentIssue false
  • English
  • Français

On convergence and quasiconformality of complex planar spline interpolants

Published online by Cambridge University Press:  24 October 2008

H. P. Dikshit  and
A. Ojha
H. P. Dikshit
Affiliation:
Department of Mathematics, R.D. University, Jabalpur 482001, India
A. Ojha
Affiliation:
Department of Mathematics, R.D. University, Jabalpur 482001, India
Get access Rights & Permissions [Opens in a new window]

Extract

There appear to be two main approaches for developing complex splines. One of these, which has been in use for quite some time, consists in defining splines on the boundary of a given region which are then extended into the interior by Cauchy's integral formula (see e.g. [1]). The other approach, which is of a more recent origin, is motivated in spirit by the theory of finite elements (see e.g. [10], p. 320) and is contained in [8] and [9]. Observing that the foregoing extension into the interior is not easy to execute numerically, certain continuous piecewise non-holomorphic functions, called complex planar splines have been studied in [8] and [9]. The choice of non-holomorphic functions is justified, since if we take the pieces to be holomorphic functions like polynomials, then by the well known identity theorem ([5], p. 132, theorem 60) the continuity of such a piecewise function implies that all the pieces represent just one holomorphic function. Thus, we shall consider polynomials in z and its conjugate z¯ of the form

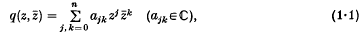
which are generally non-holomorphic functions. The number

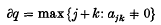
will be called the degree of q. For simplicity we also write q(z) for q(z, z¯).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 2 , March 1986 , pp. 347 - 356
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ahlberg, J. H., Nilson, E. N. and Walsh, J. L.. Complex cubic splines. Trans. Amer. Math. Soc. 129 (1967), 391–413.CrossRefGoogle Scholar
[2]Ahlfors, L. V.. Lectures on Quasiconformal Mappings, Van Nostrand Mathematical Studies vol. 10 (1966).Google Scholar
[3]de Boor, C.. A Practical Guide to Splines (Springer-Verlag, 1978).CrossRefGoogle Scholar
[4]Ciarlet, P. G. and Raviart, P. A.. General lagrange and hermite interpolation in ℝn with applications to finite element methods. Arch. Rational Mech. Anal. 46 (1972), 177–199.CrossRefGoogle Scholar
[5]Diederich, K. and Remmert, R.. Funktionentheorie I (Springer-Verlag, 1972).Google Scholar
[6]Lehto, O. and Virtanen, K. I.. Quasikonforme Abbildungen (Springer-Verlag, 1965).CrossRefGoogle Scholar
[7]Martio, O., Rickman, S. and Väisälä, J.. Definitions for quasiregular mappings. Ann. Acad. Sci. Fenn. Ser. A I Math. 448 (1969).Google Scholar
[8]Opfer, G. and Puri, M. L.. Complex planar splines. J. Approx. Theory 31 (1981), 383–402.CrossRefGoogle Scholar
[9]Opfer, G. and Schober, G.. On convergence and quasiregularity of interpolating complex planar splines. Math. Z. 180 (1982), 469–481.CrossRefGoogle Scholar
[10]Schwarz, H. R.. Methode der Finiten Elemente (Teubner, 1980).Google Scholar