Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T14:29:42.112Z Has data issue: false hasContentIssue false
  • English
  • Français

On Cheng's eigenvalue comparison theorem

Published online by Cambridge University Press:  01 May 2008

G. P. BESSA  and
J. F. MONTENEGRO
G. P. BESSA
Affiliation:
Department of Mathematics, Universidade Federal do Ceará, 60455-760 Fortaleza-CE, Brazil. e-mail: [email protected], [email protected]
J. F. MONTENEGRO
Affiliation:
Department of Mathematics, Universidade Federal do Ceará, 60455-760 Fortaleza-CE, Brazil. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We observe that Cheng's Eigenvalue Comparison Theorem for normal geodesic balls [4] is still valid if we impose bounds on the mean curvature of the distance spheres instead of bounds on the sectional and Ricci curvatures. In this version, there is a weak form of rigidity in case of equality of the eigenvalues. Namely, equality of the eigenvalues implies that the distance spheres of the same radius on each ball has the same mean curvature. On the other hand, we construct smooth metrics 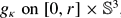, non-isometric to the standard metric canκ of constant sectional curvature κ, such that the geodesic balls 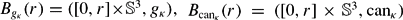have the same first eigenvalue, the same volume and the distance spheres 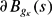and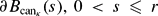, have the same mean curvatures. In the end, we apply this version of Cheng's Eigenvalue Comparison Theorem to construct examples of Riemannian manifolds M with arbitrary topology with positive fundamental tone λ*(M)>0 extending Veeravalli's examples,[7]

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 3 , May 2008 , pp. 673 - 682
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barta, J.. Sur la vibration fundamentale d'une membrane. C. R. Acad. Sci. 204 (1937), 472–473.Google Scholar
[2]Pacelli Bessa, G. and Montenegro, J. F.. An extension of Barta's theorem and geometric applications. To appear Ann. Global Anal. Geom. ArchivX math.DG/0308099.Google Scholar
[3]Chavel, I.. Eigenvalues in Riemannian Geometry. Pure and Applied Mathematics, A Series of Monograph and Textbooks (Academic Press).Google Scholar
[4]Cheng, S. Y.. Eigenfunctions and eigenvalues of the Laplacian. Amer. Math. Soc. Proc. Sympos. Pure Math. 27 (1975), 185–193.CrossRefGoogle Scholar
[5]Cheng, S. Y.. Eigenvalue comparison theorems and its geometric applications. Math. Z. 143 (1975), 289–297.CrossRefGoogle Scholar
[6]Perelman, G.. A complete Riemannian manifold of positive Ricci curvature with Euclidean volume growth and nonunique asymptotic cone. Comparison Geometry. Math. Sci. Res. Inst. Publ. 30 (1997), 165–166.Google Scholar
[7]Veeravalli, A. R.. Une remarque sur l'inégalité de McKean. Comment. Math. Helv. 78 (2003), 884–888.CrossRefGoogle Scholar