Domb and Salter (3) have postulated that the Debye characteristic temperature for the rare gas solids should be given by where C involves atomic constants and the atomic mass of the rare gas, r is the mean interatomic distance and Φ(r) is the interatomic potential. This formula provides a good approximation for the heavier rare gas solids but breaks down for the lighter inert elements. On the basis of Born's argument (1) that the dynamic rather than the static equilibrium positions should be considered, Domb (2) suggested that (1) might be replaced by 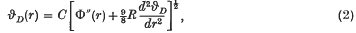, where the additional term is effectively the zero-point energy contribution to the lattice equilibrium. (R is the gas constant.) From experimental measurements of the Gruneisen parameter γ Domb obtained numerical values 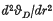which, when substituted in the right-hand side of (2), yielded values of vD that appeared to compare favourably with direct experiments. More recently Hooton (6) considered the problem of lattice dynamics with anharmonic forces (which are the dominant factor in the lighter rare gas solids) and developed a theoretical argument which also led to Domb's equation (2).