Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Takács, Lajos
1965.
A moment problem.
Journal of the Australian Mathematical Society,
Vol. 5,
Issue. 4,
p.
487.
Takács, L.
1966.
Stochastic Process: Problems and Solutions.
p.
28.
Takács, Lajos
1967.
On the Method of Inclusion and Exclusion.
Journal of the American Statistical Association,
Vol. 62,
Issue. 317,
p.
102.
Brandt, Andreas
Brandt, Manfred
and
Sulanke, Hannelore
1990.
A representation of a discrete distribution by its binomial moments.
Journal of Applied Probability,
Vol. 27,
Issue. 1,
p.
208.
Brandt, Andreas
Brandt, Manfred
and
Sulanke, Hannelore
1990.
A representation of a discrete distribution by its binomial moments.
Journal of Applied Probability,
Vol. 27,
Issue. 1,
p.
208.
Galambos, Janos
and
Xu, Yuan
1990.
A new method for generating Bonferroni-type inequalities by iteration.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 107,
Issue. 3,
p.
601.
2006.
A Course on Queueing Models.
Vol. 20066643,
Issue. ,
p.
386.


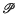 (η
(η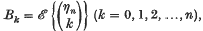 , the binomial moments of η
, the binomial moments of η