Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T11:45:33.277Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on orthogonality and permutability of subnormal subgroups

Published online by Cambridge University Press:  24 October 2008

John C. Lennox
John C. Lennox
Affiliation:
University College, Cardiff
Get access Rights & Permissions [Opens in a new window]

Extract

Let H and K be groups with derived sub groups H´ and K´. Following (5) we say that H and K are orthogonal, and write H ⊥ K, if and only if the tensor product H/H´ ®K/K´ is trivial. If H and K are sub groups of a group we say that H and K permute if and only if HK = KH. We recall finally that the subgroup H of the group G is said to be subnormal in G, written H sn G, if and only if there exists a finite chain of subgroups

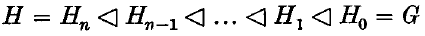
connecting H to G.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 72 , Issue 3 , November 1972 , pp. 351 - 355
Copyright
Copyright © Cambridge Philosophical Society 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Fuchs, L.Abelian Groups (Pergamon, Oxford, 1960).Google Scholar
(2)Lennox, J. C. Ph.D. Dissertation (Cambridge, 1970).Google Scholar
(3)Robinson, D. S.Joins of subnormal subgroups. Illinois J. Math. 9 (1965), 144–168.CrossRefGoogle Scholar
(4)Roseblade, J. E.On certain subnormal coalition classes. J. Algebra (2), 1 (1964), 132–138.CrossRefGoogle Scholar
(5)Roseblade, J. E.The permutabiity of orthogonal subnormal subgroups. Math. Z. 90 (1965), 365–372.CrossRefGoogle Scholar
(6)Roseblade, J. E. and Stonehewer, S. E.Subjunctive and locally coalescent classes of groups. J. Algebra (8), 4 (1967), 423–438.Google Scholar
(7)Roseblade, J. E.The derived series of a join of subnormal subgroups. Math. Z. 117 (1970), 57–59.CrossRefGoogle Scholar
(8)Wielandt, H.Vertauschbare Nachinvariante Untergruppen. Abh. Math. Sem. Univ. Hamburg 21 (1957), 55–62.CrossRefGoogle Scholar
(9)Wielandt, H.Topics in the theory of composite groups. University of Wisconsin Lecture Notes, 1967.Google Scholar