Published online by Cambridge University Press: 24 October 2008
Let N > 1 and let AN be the polydisc algebra, i.e. the algebra of all continuous functions on the closed polydisc δ¯N ⊂ 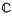 N, analytic on the open polydisc δN, with sup norm. Call a closed set F ⊂ δ¯N a peak interpolation set for AN if given any f ε C(F), f ≠ 0, there is an extension f ε AN of f such that ¦f˜(z)¦ < ‖ f ‖ (z ε δ¯N - F); call F a norm preserving interpolation set for AN if given any f ε C(F) there is an extension f˜ ε AN of f such that ‖f˜‖ = ‖f‖. The paper gives a complete description of norm preserving interpolation sets for AN in terms of peak interpolation sets for AM, M ≤ N.
N, analytic on the open polydisc δN, with sup norm. Call a closed set F ⊂ δ¯N a peak interpolation set for AN if given any f ε C(F), f ≠ 0, there is an extension f ε AN of f such that ¦f˜(z)¦ < ‖ f ‖ (z ε δ¯N - F); call F a norm preserving interpolation set for AN if given any f ε C(F) there is an extension f˜ ε AN of f such that ‖f˜‖ = ‖f‖. The paper gives a complete description of norm preserving interpolation sets for AN in terms of peak interpolation sets for AM, M ≤ N.