Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T14:11:39.706Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-existence of standing modes in certain problems of linear elasticity

Published online by Cambridge University Press:  24 October 2008

R. D. Gregory
R. D. Gregory
Affiliation:
University of Manchester
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that an elastic half-space, which contains certain surface defects, inclusions and cavities, is in free, two-dimensional, time-harmonic vibration, with the wave field at infinity ‘outgoing’ in character. It is shown that the elastic potentials representing such a ‘standing mode’ can be expressed in the form of contour integrals, for instance

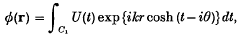
U(t) being an analytic function of t. By considering the far field of these potentials, it is shown that U(t) is zero on a certain arc in the t-plane and is therefore identically zero. It follows that ø(r) is zero everywhere and this proves the non-existence of such standing modes in these configurations.

This uniqueness theorem justifies the solution given by the author (Gregory (2)) for the problem in which time harmonic stresses act on the walls of a cylindrical cavity lying beneath the surface of an elastic half-space. It is also shown that if a Rayleigh surface wave is incident on any system of surface defects, inclusions and cavities, then energy must be transferred from the surface wave to scattered outgoing body waves of both P and S types.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 2 , March 1975 , pp. 385 - 404
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Gregory, R. D.An expansion theorem applicable to problems of wave propagation in an elastic half-space containing a cavity. Proc. Cambridge Philos. Soc. 63 (1967), 1341–1367.CrossRefGoogle Scholar
(2)Gregory, R. D.The propagation of waves in an elastic half-space containing a cylindrical cavity. Proc. Cambridge Philos. Soc. 67 (1970), 689–710.CrossRefGoogle Scholar
(3)Gregory, R. D. Ph.D. Thesis, University of Manchester 1967.Google Scholar
(4)Jeffreys, H.Asymptotic approximations (Oxford Clarendon Press, 1962).Google Scholar
(5)John, F.On the motion of floating bodies. II. Comm. Pure Appl. Math. 3 (1950), 153–158.CrossRefGoogle Scholar
(6)Kupradze, V. D.Dynamical problems in elasticity; progress in solid mechanics, vol. 3 (Wiley, 1963).Google Scholar
(7)Smithies, F.Integral equations (Cambridge University Press, 1962).Google Scholar
(8)Ursell, F.Surface waves on deep water in the presence of a submerged circular cylinder. II. Proc. Cambridge Philos. Soc. 46 (1950), 153–158.CrossRefGoogle Scholar
(9)Ursell, F.Trapping modes in the theory of surface waves. Proc. Cambridge Philos. Soc. 47 (1951), 347–358.CrossRefGoogle Scholar
(10)Wheeler, L. T. and Sternberg, E.Some theorems in classical elastodynamics. Arch. Rational Mechanics and Analysis 31 (1968), 51–90.CrossRefGoogle Scholar
(11)Wilcox, C. A.A generalisation of theorems of Rellich and Atkinson. Proc. Amer. Math. Soc. 7 (1956), 271–276.CrossRefGoogle Scholar