Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2025-01-05T00:58:41.120Z Has data issue: false hasContentIssue false
  • English
  • Français

A new generating function for Jacobi polynomials

Published online by Cambridge University Press:  24 October 2008

R. K. Saxena
R. K. Saxena
Affiliation:
Department of Mathematics, McGill University Montreal, Canada†
Get access Rights & Permissions [Opens in a new window]

Extract

In an earner paper ((6), p. 209) the author has given a generating function for the Jacobi polynomials defined by ((5), p. 254)

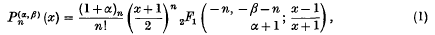
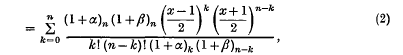
In the present note we obtain another generating function for these polynomials. The results given earlier by Manocha and Sharma ((4), p. 432) in these proceedings and Brafman in (2) follow as a particular case of our result.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 2 , September 1969 , pp. 345 - 347
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Appell, P. and Kampé de Fériet, J.Fonctions hypergéométriques et hyperaphériques polynomes d' Hermiie (Gauthier-Villars; Paris, 1926).Google Scholar
(2)Brafman, F.Generating function of Jacobi and related polynomials. Proc. Amer. Math. Soc. 2 (1951), 942–949.Google Scholar
(3)Byrchnall, J. L.Differential equations associated with hypergeometric functions. Quart. J. Math. Oxford 13 (1942), 90–106.CrossRefGoogle Scholar
(4)Manocha, H. L. and Sharma, B. L.Generating functions of Jacobi polynomials. Proc. Cambridge Philos. Soc. 63 (1967), 431–433.CrossRefGoogle Scholar
(5)Rainville, E. D.Special functions (Macmillan; New York, 1960).Google Scholar
(6)Saxena, R. K.A generating function for Jacobi polynomials. Canad. Math. Bull. 9 (1966), 209–214.CrossRefGoogle Scholar