Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-03T02:38:44.230Z Has data issue: false hasContentIssue false
  • English
  • Français

The multifractal nature of heterogeneous sums of Dirac masses

Published online by Cambridge University Press:  01 May 2008

JULIEN BARRAL  and
STÉPHANE SEURET
JULIEN BARRAL
Affiliation:
INRIA Rocquencourt, B.P. 105, 78153 Le Chesnay Cedex, France. e-mail: [email protected]
STÉPHANE SEURET
Affiliation:
INRIA Rocquencourt, B.P. 105, 78153 Le Chesnay Cedex, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

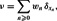This paper investigates the natural problem of performing the multifractal analysis of heterogeneous sums of Dirac masseswhere (xn)n≥0 is a sequence of points in [0, 1]d and (wn)n≥0 is a positive sequence of weights such that Σn≥0wn < ∞. We consider the case where the points xn are roughly uniformly distributed in [0, 1]d, and the weights wn depend on a random self-similar measure μ, a parameter ρ ∈ (0, 1], and a sequence of positive radii (λn)n≥1 converging to 0 in the following way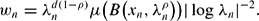The measure ν has a rich multiscale structure. The computation of its multifractal spectrum is related to heterogeneous ubiquity properties of the system {(xn,λn)n with respect to μ.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 3 , May 2008 , pp. 707 - 727
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arbeiter, M. and Patzschke, N.. Random self-similar multifractals. Math. Nachr. 181 (1996), 5–42.Google Scholar
[2]Aversa, V. and Bandt, C.. The multifractal spectrum of discrete measures. Acta Univ. Car. 31 (21) (1990), 5–8.Google Scholar
[3]Bacry, E. and Muzy, J.-F., Log-infinitely divisible multifractal processes. Commun. Math. Phys. 236 (2003), 449–475.CrossRefGoogle Scholar
[4]Barral, J.. Continuity of the multifractal spectrum of random statistically self-similar measures. J. Theoret. Probab. 13 (2000), 1027–1060.Google Scholar
[5]Barral, J., Nasr, F. Ben and Peyriére, J.. Comparing multifractal formalisms: the neighboring condition. Asian J. Math. 7 (2003), 149–166.Google Scholar
[6]Barral, J. and Mandelbrot, B.. Multifractal products of cylindrical pulses. Probab. Theory Related Fields 124 (2002), 409–430.Google Scholar
[7]Barral, J. and Mandelbrot, B.. Random multiplicative multifractal measures. In Fractal Geometry and Applications: A {J}ubilee of Benoit Mandelbrot, Proc. Sympos. Pure Math. 72, Part 2, (2004), pp 3–90.Google Scholar
[8]Barral, J. and Seuret, S.. Combining multifractal additive and multiplicative chaos. Commun. Math. Phys. 257 (2005), 473–497.Google Scholar
[9]Barral, J. and Seuret, S.. Inside singularity sets of random Gibbs measures. J. Stat. Phys. 120 (5-6) (2005), 1101–1124.Google Scholar
[10]Barral, J. and Seuret, S.. Renewal of singularity sets of statistically self-similar measures. Adv. Appl. Prob., 39 (2007), 162–188.CrossRefGoogle Scholar
[11]Barral, J. and Seuret, S.. Heterogeneous ubiquitous systems in Rd and Hausdorff dimension. Bull. Braz. Math. Soc., 38 (2007), 467–515.Google Scholar
[12]Bertoin, J.. Lévy Processes (Cambridge University Press, 1996).Google Scholar
[13]Brown, G., Michon, G. and Peyriére, J.. On the multifractal analysis of measures. J. Stat. Phys. 66 (1992), 775–790.Google Scholar
[14]Dodson, M. M., Melián, M. V.., Pestana, D. and Vélani, S. L.. Patterson measure and Ubiquity. Ann. Acad. Sci. Fenn. Ser. A I Math. 20, 37–60 (1995).Google Scholar
[15]Falconer, K. J.. The multifractal spectrum of statistically self-similar measures. J. Theoret. Prob. 7 (1994), 681–702.Google Scholar
[16]Falconer, K. J.. Representation of families of sets by measures, dimension spectra and Diophantine approximation. Math. Proc. Camb. Phil. Soc. 128 (2000), 111–121.Google Scholar
[17] A.Fan, H.. Multifractal analysis of infinite products. J. Stat. Phys. 86 (1997), 5/6: 1313–1336.Google Scholar
[18]Holley, R. and Waymire, E. C.. Multifractal dimensions and scaling exponents for strongly bounded random fractals. Ann. Appl. Probab. 2 (1992), 819–845.Google Scholar
[19]Jaffard, S.. Old friends revisited: The multifractal nature of some classical functions. J. Fourier Anal. Appl. 3 (1997), 1–22.Google Scholar
[20]Jaffard, S.. The multifractal nature of Lévy processes. Probab. Theory Related Fields 114 (1999), 207–227.CrossRefGoogle Scholar
[21]Kahane, J. -P.. Positive martingales and random measures. Chinese. Ann. Math. 8B1 (1987), 1–12.Google Scholar
[22]Kifer, Y.. Fractals via random iterated function systems and random geometric constructions, Fractal geometry and stochastics (Finsterbergen, 1994). Progr. Probab. 37 (1995), 145–164.Google Scholar
[23]Kahane, J.-P. and Peyriére, J.. Sur certaines martingales de Benoit M andelbrot. Adv. in Math. 22 (1976), 131–145.Google Scholar
[24]F, J.. Kingman, C.. Completely random measures. Pacific J. Math. 21 (1967), 59–78.Google Scholar
[25]Lévy Véhel, J. and Vojak, R.. Multifractal analysis of {C}hoquet capacities. Adv. Appl. Math. 20 (1998), 1–43.Google Scholar
[26]Liu, Q.. On generalized multiplicative cascades. Stochastic Process. Appl. 86 (2000), 263–286.Google Scholar
[27]Mandelbrot, B. M.. Intermittent turbulence in self-similar cascades: divergence of high moments and dimension of the carrier. J. Fluid Mech. 62 (1974), 331–358.Google Scholar
[28]Molchan, G. M.. Scaling exponents and multifractal dimensions for independent random cascades. Commun. Math. Phys. 179 (1996), 681–702.CrossRefGoogle Scholar
[29]Olsen, L.. Random geometrically graph directed self-similar multifractals. Pitman Research Notes in Mathematics Series. 307 (1994).Google Scholar
[30]Olsen, L.. A multifractal formalism. Adv. Math. (1995) 116, 92–195.Google Scholar
[31]Olsen, L.. Self-affine multifractal Sierpinski sponges in Rd. Pacific J. Math., 183 (1998).Google Scholar
[32]Pesin, Y. and Weiss, H.. The multifractal analysis of Gibbs measures: motivation, mathematical foundation, and examples. Chaos 7 (1) (1997), 89–106.Google Scholar
[33]Parry, W. and Policott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque (1990), 187–188.Google Scholar