Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nishimura, T.
Oset Sinha, R.
Ruas, M. A. S.
and
Wik Atique, R.
2016.
Liftable vector fields over corank one multigerms.
Mathematische Annalen,
Vol. 366,
Issue. 1-2,
p.
573.


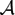 -simple germs from
-simple germs from 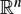 to
to