Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T15:00:32.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Locally finite approximation of Lie groups. II

Published online by Cambridge University Press:  24 October 2008

Eric M. Friedlander  and
Guido Mislin
Eric M. Friedlander
Affiliation:
Northwestern University, Evanston, IL 60201, U.S.A.
Guido Mislin
Affiliation:
Eidgenössische Technische Hochschule, 8092 Zürich, Switzerland
Get access Rights & Permissions [Opens in a new window]

Extract

In an earlier paper [10], we constructed a ‘locally finite approximation away from a given prime p’ of the classifying space BG of a Lie group with finite component group. Such an approximation consists of a locally finite group g and a homotopy class of maps 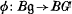which in particular induces an isomorphism in cohomology with finite coefficients of order prime to p. The usefulness of such a construction is that it reduces various homotopy-theoretic questions concerning the space BG to the corresponding questions concerning Bπ for finite subgroups π. For example, we demonstrated in [10] how H. Miller's proof of the Sullivan conjecture concerning maps from 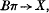, where π is a finite group and X is a finite-dimensional complex, can be extended to maps BG→X for G a Lie group with finite component group.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 100 , Issue 3 , November 1986 , pp. 505 - 517
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, J. F.. Stable Homotopy and Generalised Homology. Chicago Lectures in Math. (University of Chicago Press, 1974).Google Scholar
[2]Atiyah, M. F. and Segal, G. B.. Equivariant K-theory and completion. J. Differential Geom. 3 (1967), 1–18.Google Scholar
[3]Benson, D.. Modular Representation Theory: New Trends and Methods. Lecture Notes in Math. 1081 (Springer-Verlag, 1984).Google Scholar
[4]Borel, A.. On proper actions and maximal compact subgroups of locally compact groups (to appear).Google Scholar
[5]Cartan, H. and Eilenberg, S.. Homological Algebra (Princeton University Press, 1956).Google Scholar
[6]Carlsson, G.. Equivariant stable homotopy and Segal's Burnside ring conjecture. Ann. of Math 120 (1984), 189–224.CrossRefGoogle Scholar
[7]Curtis, C. W. and Reiner, I.. Methods of Representation Theory with Applications to Finite Groups and Orders. Volume 1 (Wiley-Interscience, 1981).Google Scholar
[8]Demazure, M. and Gabriel, P.. Introduction to Algebraic Geometry and Algebraic Groups. North-Holland Mathematical Studies 39 (North-Holland, 1980).Google Scholar
[9]Fesbach, M.. The Segal Conjecture for compact Lie groups (to appear).Google Scholar
[10]Friedlander, E. M. and Mislin, G.. Locally finite approximation of Lie groups, I. Inventiones Math. 83 (1986), 425–436.Google Scholar
[11]Madsen, I.. Smooth spherical space forms. In Geometric Applications of Homotopy Theory, Lecture Notes in Math. vol. 657 (Springer-Verlag, 1978), 303–352.Google Scholar
[12]Meier, W.. Localisation, complétion, et applications fantômes. C.R. Acad. Sci. Paris 281, Serie A (1975), 787–789.Google Scholar
[13]Meier, W.. Détermination de certaines groupes d'applications fantômes. C.R. Acad. Sci. Paris 283, Serie A (1976), 971–974.Google Scholar
[14]Miller, H.. The Sullivan Conjecture on maps from classifying spaces. Ann. of Math 120 (1984), 39–87.CrossRefGoogle Scholar
[15]Milne, J.. Etale Cohomology (Princeton University Press, 1980).Google Scholar
[16]Quillen, D.. The spectrum of an equivariant cohomology ring, I, II. Ann. of Math 94 (1971), 549–602.Google Scholar
[17] Séminaire de Géométric Algébrique (SGA3). Schémas en Groupes I, III. Lecture Notes in Math. vol. 151, 153 (Springer-Verlag, 1970).Google Scholar
[18]Serre, J.-P.. Représentations Linéaires des Groupes Finis (Hermann, Paris, 1967).Google Scholar
[19]Springer, T. A. and Steinberg, R.. Conjugacy classes. In Seminar on Algebraic Groups and Related Finite Groups, Lecture Notes in Math. vol. 131 (Springer-Verlag, 1970), 167–266.Google Scholar
[20]Zabrodsky, A.. Maps between classifying spaces (to appear).Google Scholar