Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T13:53:16.437Z Has data issue: false hasContentIssue false
  • English
  • Français

Linking sandwich pairs

Published online by Cambridge University Press:  15 June 2009

MARTIN SCHECHTER
MARTIN SCHECHTER*
Affiliation:
Department of Mathematics, University of California, Irvine, CA 92697-3875, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Since the development of the calculus of variations there has been interest in finding critical points of functionals. This was intensified by the fact that for many equations arising in practice, the solutions are critical points. In searching for critical points, there is a distinct advantage if the functional G is semibounded. In this case one can find a Palais–Smale (PS) sequenceor even a Cerami sequence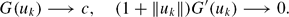These sequences produce critical points if they have convergent subsequences. However, there is no clear method of finding critical points of functionals which are not semibounded. Linking subsets do provide such a method. They can produce a PS sequence provided they separate the functional. In the present paper we show that there are pairs of subsets that can produce Cerami-like sequences even though they do not separate the functional. All that is required is that the functional be bounded from above on one of the sets and bounded from below on the other, with no relationship needed between the bounds. This provides a distinct advantage in applications. We apply the method to several situations.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 147 , Issue 3 , November 2009 , pp. 679 - 700
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, R. A.Sobolev Spaces (Academic Press, 1975).Google Scholar
[2]Bartolo, P., Benci, V. and Fortunato, D.Abstract critical applications to some nonlinear problems with “strong” resonance at infinity. Nonlinear Anal. 7 (1983) 981–1012.CrossRefGoogle Scholar
[3]Cerami, G.An existence criterion for the critical points on unbounded manifolds. (Italian) Istit. Lombardo Accad. Sci. Lett. Rend. A 112 (1978), no. 2, (1979), 332–336.Google Scholar
[4]Costa, D. G. and Magalhães, C. A.Variational elliptic problems which are nonquadratic at infinity. Nonlinear Anal. 23 (1994), no. 11, 1401–1412.CrossRefGoogle Scholar
[5]Furtado, M. F., Maia, L. A. and Silva, E. A. B.On a double resonant problem in N. Differential Integral Equations 15 (2002), no. 11, 1335–1344.CrossRefGoogle Scholar
[6]Furtado, M. F. and Silva, E. A. B. Double resonant problems which are locally non-quadratic at infinity. Proceedings of the USA-Chile Workshop on Nonlinear Analysis (Vi-a del Mar-Valparaiso, 2000), 155–171 (electronic). Electron. J. Differ. Equ. Conf., 6 (Southwest Texas State Univ., San Marcos, TX, 2001).Google Scholar
[7]Schechter, M.New saddle point theorems. Generalized functions and their applications (Varanasi, 1991), 213–219 (Plenum, 1993).CrossRefGoogle Scholar
[8]Schechter, M.A generalization of the saddle point method with applications. Ann. Polon. Math. 57 (1992), no. 3, 269–281.CrossRefGoogle Scholar
[9]Schechter, M.New linking theorems. Rend. Sem. Mat. Univ. Padova 99 (1998), 255–269.Google Scholar
[10]Schechter, M.Linking Methods in Critical Point Theory (Birkhauser, 1999).CrossRefGoogle Scholar
[11]Schechter, M.Sandwich pairs in critical point theory. Trans. Amer. Math. Soc. 360 (2008), no. 6, 2811–2823.CrossRefGoogle Scholar
[12]Schechter, M. Semilinear problems in critical point theory, to appear.Google Scholar
[13]Schechter, M.The use of Cerami sequences in critical point theory theory. Abstr. Appl. Anal. 2007, (2007) Art. ID 58948, 28 pp.CrossRefGoogle Scholar
[14]Silva, E. A. de B. e.Linking theorems and applications to semilinear elliptic problems at resonance. Nonlinear Anal. 16 (1991), 455–477.CrossRefGoogle Scholar