Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T14:18:00.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear forms in algebraic points of Abelian functions. I

Published online by Cambridge University Press:  24 October 2008

D. W. Masser
D. W. Masser
Affiliation:
University of Nottingham
Get access Rights & Permissions [Opens in a new window]

Extract

Let Ω be a Riemann matrix whose 2n columns are vectors of Cn. It is well-known (e.g. (10)) that the field 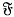of meromorphic functions on Cn with these vectors among their periods is of transcendence degree n over C. More precisely, this field can be written as C(A, B) where A = (A1, …, An) is a vector of algebraically independent functions of the variable z = (z1, …, zn) and B is algebraic over C(A). We shall assume that B is in fact integral of degree d over the ring C[A]. Since the derivatives ∂f/∂zi of a periodic function f(z) are also periodic, the field 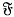is mapped into itself by the differential operators ∂/∂zi. Thus there exists a function C(z) in C[A] such that these operators map the ring C[A, B, C−1] into itself.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 3 , May 1975 , pp. 499 - 513
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, A.Linear forms in the logarithms of algebraic numbers. Mathematika 13 (1966), 204–216.CrossRefGoogle Scholar
(2)Bombieri, E.Algebraic values of meromorphic maps. Invent. Math. 10 (1970), 267–287.CrossRefGoogle Scholar
(3)Cassels, J. W. S.An introduction to diophantine approximation. (Cambridge, 1957.)Google Scholar
(4)Gelfond, A. O.Transcendental and algebraic numbers. (New York: Dover, 1960.)Google Scholar
(5)Landau, E.Einführung in die elementare und analytische Theorie der algebraischen Zahlen und der Ideale. (Leipzig: Teubner, 1918.)Google Scholar
(6)Lang, S.Introduction to transcendental numbers. (Reading: Addison-Wesley, 1966.)Google Scholar
(7)Masser, D. W. Elliptic functions and transcendence. Ph.D. thesis, University of Cambridge, 1974 (to appear in the Springer Lecture Notes series).CrossRefGoogle Scholar
(8)Roth, K. F.Rational approximations to algebraic numbers. Mathematika 2 (1955), 1–20.CrossRefGoogle Scholar
(9)Schneider, T.Einführung in die transzendenten Zahlen. (Berlin: Springer-Verlag, 1957.)CrossRefGoogle Scholar
(10)Siegel, C. L.Topics in complex function theory vol. III. (New York: Wiley-Interscience, 1973.)Google Scholar