Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T18:21:39.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrangian submanifolds satisfying a basic equality

Published online by Cambridge University Press:  24 October 2008

Bang-Yen Chen  and
Luc Vrancken
Bang-Yen Chen
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, Michigan 48824-1027 U.S.A. E-mail address: [email protected]
Luc Vrancken
Affiliation:
Departement Wiskunde, Celestijnenlaan 200 B, B-3001 Leuven, Belgium e-mail address: luc.vrancken©wis.kuleuven.ac.be
Get access Rights & Permissions [Opens in a new window]

Abstract

In [3], B. Y. Chen proved that, for any Lagrangian submanifold M in a complex space-form Mn(4c) (c = ± 1), the squared mean curvature and the scalar curvature of M satisfy the following inequality:

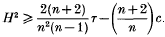
He then introduced three families of Riemannian n-manifolds 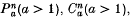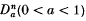and two exceptional n-spaces Fn, Ln and proved the existence of a Lagrangian isometric immersion pa from 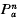into ℂPn(4) and the existence of Lagrangian isometric immersions f, l, ca, da from Fn, Ln, 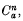, 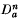into ℂHn(− 4), respectively, which satisfy the equality case of the inequality. He also proved that, beside the totally geodesie ones, these are the only Lagrangian submanifolds in ℂPn(4) and in ℂHn(− 4) which satisfy this basic equality. In this article, we obtain the explicit expressions of these Lagrangian immersions. As an application, we obtain new Lagrangian immersions of the topological n-sphere into ℂPn(4) and ℂHn(−4).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 2 , August 1996 , pp. 291 - 307
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bolton, J., Jensen, G. R., Rigoli, M. and Woodward, L. M.. On conformal minimal immersions of S 2 into ℂPn. Math. Ann. 279 (1988), 599–620.CrossRefGoogle Scholar
[2]Chen, B. Y.. Total mean curvature and submanifolds of finite type (World Scientific, 1984).CrossRefGoogle Scholar
[3]Chen, B. Y.. Jacobi's elliptic functions and Lagrangian immersions. Proc. Royal Soc. Edinburgh Sect. A, Math. 126 (1996) (to appear).Google Scholar
[4]Chen, B. Y., Dillen, F., Verstraelen, L. and Vrancken, L.. An exotic totally real minimal immersion of S 3 in ℂP3 and its characterization. Proc. Royal Soc. Edinburgh Sect. A, Math. 126 (1996) (in press).Google Scholar
[5]Chen, B. Y., Ludden, G. D. and Montiel, S.. Real submanifolds of a Kaehlerian manifold. Algebra, Groups and Geometries 1 (1984), 176–212.Google Scholar
[6]Lawden, D. F., Elliptic functions and applications (Springer–Verlag, 1989).CrossRefGoogle Scholar
[7]Reckziegel, H.. Horizontal lifts of isometric immersions into the bundle space of a pseudo-Riemannian submersion; in Global differential geom and global analysis (1984). Lecture Notes in Mathematics (Springer-Verlag, 1985), pp. 264–279.Google Scholar