Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-16T22:24:46.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups of automorphisms of Abelian 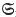1-groups

Published online by Cambridge University Press:  24 October 2008

B. Hartley
B. Hartley
Affiliation:
University of Warwick, Coventry
Get access Rights & Permissions [Opens in a new window]

Extract

Following Robinson(4), we shall use the term Abelian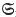1-group to describe an Abelian group A of finite (Mal'cev special or Prüfer) rank, whose torsion subgroup T is Černikov. These groups were called Abelian groups of type A3 by Mal'cev (3). Let G = Aut A. It is not hard to see that G/CG(A/T) and G/CG(T) are linear groups, and CG(A/T) ∩ CG(T) is Abelian. We improve on this observation by proving

Theorem 1. The group G contains a normal Abelian Černikov subgroup G0, such that G/G0is linear over a field of characteristic zero.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 2 , March 1975 , pp. 241 - 245
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hartley, B. and Tomkinson, M. J.Splitting over nilpotent and hypercentral residuals. Submitted to Math. Proc. Cambridge Philos. Soc.Google Scholar
(2)Kaplansky, I.Infinite abelian groups (University of Michigan, Ann Arbor, 1954).Google Scholar
(3)Mal'cev, A. I.On certain classes of infinite soluble groups. Mat. Sb. 28 (1951), 567–588 (Russian); Translations Amer. Math. Soc. (2) 2 (1956), 1–21.Google Scholar
(4)Robinson, Derek J. S.Finiteness conditions and generalized soluble groups, Parts 1 and 2 (Ergebnisse der Math. und ihrer Grenzgebiete, Vols. 62, 63, Springer-Verlag, Berlin, 1972).Google Scholar
(5)Wehrfritz, B. A. F.Infinite linear groups (Ergebnisse der Math. und ihrer Grenzgebiete, Vol. 76, Springer-Verlag, Berlin, 1973).CrossRefGoogle Scholar