Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T22:23:08.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry of the tensor product of C*-algebras

Published online by Cambridge University Press:  24 October 2008

D. P. Blecher
D. P. Blecher
Affiliation:
Department of Mathematics, University of Edinburgh, Edinburgh EH9 3JZ
Get access Rights & Permissions [Opens in a new window]

Extract

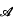When and ℬ are C*-algebras their algebraic tensor product 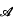⊗ ℬ is a *-algebra in a natural way. Until recently, work on tensor products of C*-algebras has concentrated on norms α which make the completion 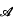⊗α ℬ into a C*-algebra. The crucial role played by the Haagerup norm in the theory of operator spaces and completely bounded maps has produced some interest in more general norms (see [8; 12]). In this paper we investigate geometrical properties of algebra norms on 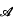⊗ ℬ. By an ‘algebra norm’ we mean a norm which is sub-multiplicative: α(u.v) ≤ ≤ α(u).α(v).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 1 , July 1988 , pp. 119 - 127
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bonsall, F. F. and Duncan, J.. Complete Normed Algebras (Springer-Verlag, 1973).CrossRefGoogle Scholar
[2]Bonsall, F. F. and Duncan, J.. Numerical Ranges of Operators on Normed Spaces and Elements of Normed Algebras (Cambridge University Press, 1971).CrossRefGoogle Scholar
[3]Carne, T. K.. Tensor products and Banach algebras. J. London Math. Soc. (2) 17 (1978), 480–488.CrossRefGoogle Scholar
[4]Carne, T. K.. Not all H' algebras are operator algebras. Math. Proc. Cambridge Philos. Soc. 86 (1979), 243–249.CrossRefGoogle Scholar
[5]Carne, T. K.. Representation theory for tensor products of Banach algebras. Math. Proc. Cambridge Philos. Soc. 90 (1981), 445–463.CrossRefGoogle Scholar
[6]Choi, M. D. and Effros, E. G.. Nuclear C*-algebras and the approximation property. Amer. J. Math. 100 (1978), 61–79.CrossRefGoogle Scholar
[7]Dixmier, J.. C*-algebras (North-Holland, 1977).Google Scholar
[8]Effros, E. G. and Kishimoto, A.. Module maps and Hochschild–Johnson cohomology. Preprint (1985).Google Scholar
[9]Grothendieck, A.. Produits tensoriels topologiques et espaces nucléaires. Mem. Amer. Math. Soc. 16 (1955).Google Scholar
[10]Grothendieck, A.. Résumé de la théorie métrique des produits tensoriels topologiques. Bull. Soc. Mat. Sao Paulo 8 (1956), 1–79.Google Scholar
[11]Haagerup, U.. The Grothendieck inequality for bilinear forms on C*-algebras. Adv. in Math. 56 (1985), no. 2, 93–116.CrossRefGoogle Scholar
[12]Kaijser, S. and Sinclair, A. M.. Projective tensor products of C*-algebras. Math. Scand. 65 (1984), 161–187.CrossRefGoogle Scholar
[13]Lance, C.. Tensor products of non-unital C*-algebras. J. London Math. Soc. (2), 12 (1976), 160–168.CrossRefGoogle Scholar
[14]Okayusu, T.. Some cross norms which are not uniformly cross. Proc. Japan Acad. 46 (1970). 54–57.Google Scholar
[15]Paulsen, V.. Completely Bounded Maps and Dilations (Pitman, 1986).Google Scholar
[16]Paulsen, V. and Smith, R. R.. Multilinear maps and tensor norms on operator systems. Preprint (1985).Google Scholar
[17]Takesaki, M.. Theory of Operator Algebras I (Springer-Verlag, 1979).CrossRefGoogle Scholar
[18]Torpe, A.-M.. Notes on nuclear C*-algebras and injective von Neumann algebras. Odense Universitet Matematisk Institut Preprints no. 3 (1981).Google Scholar