Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T14:17:00.855Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalized Bernstein approximation theorem

Published online by Cambridge University Press:  24 October 2008

João B. Prolla
João B. Prolla
Affiliation:
Departamento de Matemática – IMECC, Universidade Estadual de Campinas, Caixa Postal 6065, 13081 – Campinas, S.P., Brazil
Get access Rights & Permissions [Opens in a new window]

Extract

A celebrated theorem of Weierstrass states that any continuous real-valued function f defined on the closed interval [0, 1] ⊂ ℝ is the limit of a uniformly convergent sequence of polynomials. One of the most elegant and elementary proofs of this classic result is that which uses the Bernstein polynomials of f

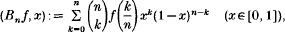
one for each integer n ≥ 1. Bernstein's Theorem states that Bn(f) → f uniformly on [0, 1] and, since each Bn(f) is a polynomial of degree at most n, we have as a consequence Weierstrass' theorem. See for example Lorentz [9]. The operator Bn, defined on the space C([0, 1]; ℝ) with values in the vector subspace of all polynomials of degree at most n has the property that Bn(f) ≥ 0 whenever f ≥ 0. Thus Bernstein's Theorem also establishes the fact that each positive continuous real-valued function on [0, 1] is the limit of a uniformly convergent sequence of positive polynomials. This raises the following natural question: consider a compact Hausdorff space X and the convex cone C+(X):= {f ∈ C(X; ℝ); f ≥ 0}. Now the analogue of Bernstein's Theorem would be a theorem stating when a convex cone contained in C+(X) is dense in it. More generally, one raises the question of describing the closure of a convex cone contained in C(X; ℝ), and, in particular, the closure of A+:= {f ∈ A; f ≥ 0}, where A is a subalgebra of C(X; ℝ).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 2 , September 1988 , pp. 317 - 330
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bishop, E.. A generalization of the Stone–Weierstrass theorem. Pacific J. Math. 11 (1961), 777–783.CrossRefGoogle Scholar
[2]Bonsall, F. F.. Semi-algebras of continuous functions. Proc. London Math. Soc. (3) 10 (1960), 122–140.CrossRefGoogle Scholar
[3]Brosowski, B. and Deutsch, F.. An elementary proof of the Stone–Weierstrass theorem. Proc. Amer. Math. Soc. 81 (1981), 89–92.CrossRefGoogle Scholar
[4]Burckel, R. B.. Bishop's Stone–Weierstrass theorem. Amer. Math. Monthly 91 (1984), 22–32.Google Scholar
[5]Ellis, A. J.. Some approximation results for function spaces. Indag. Math. 42 (1980), 125–130.CrossRefGoogle Scholar
[6]Feyel, D. and de La Pradelle, . Sur certaines extensions du Théorème d'approximation de Bernstein. Pacific J. Math. 115 (1984), 81–89.CrossRefGoogle Scholar
[7]Glicksberg, I.. Measures orthogonal to algebras and sets of antisymmetry. Trans. Amer. Math. Soc. 104 (1962), 415–435.CrossRefGoogle Scholar
[8]Jewett, R. I.. A variation on the Stone–Weierstrass theorem. Proc. Amer. Math. Soc. 14 (1963), 690–693.CrossRefGoogle Scholar
[9]Lorentz, G. G.. Approximation of Functions (Holt, Rinehart and Winston, 1966).Google Scholar
[10]Machado, S.. On Bishop's generalization of the Weierstrass–Stone theorem. Indag. Math. 39 (1977), 218–224.CrossRefGoogle Scholar
[11]Nachbin, L.. Weighted approximation for algebras and modules of continuous functions: real and self-adjoint complex cases. Ann. of Math. 81 (1965), 289–302.CrossRefGoogle Scholar
[12]Nachbin, L.. Elements of Approximation Theory (van Nostrand, 1967; reprinted, Krieger, 1976).Google Scholar
[13]von Neumann, J.. Probabilistic logics and the synthesis of reliable organisms from unreliable components. In Automata Studies (Princeton University Press, 1956), pp. 93–94.Google Scholar
[14]Prolla, J. B.. Approximation of Vector Valued Functions (North-Holland, 1977).Google Scholar
[15]Ransford, T. J.. A short elementary proof of the Bishop–Stone–Weierstrass theorem. Math. Proc. Cambridge Philos. Soc. 96 (1984), 309–311.CrossRefGoogle Scholar
[16]Shilov, G. E.. On rings of functions with uniform convergence. Ukrain. Mat. Zh. 3 (1951), 404–411.Google Scholar