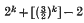Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
van der Poorten, Alfred J.
1976.
On Baker's inequality for linear forms in logarithms.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 80,
Issue. 2,
p.
233.
van der Poorten, A. J.
1976.
Hermite interpolation andp-adic exponential polynomials.
Journal of the Australian Mathematical Society,
Vol. 22,
Issue. 1,
p.
12.
Beukers, F.
1981.
Fractional parts of powers of rationals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 90,
Issue. 1,
p.
13.
Bennett, M.
1993.
Fractional parts of powers of rational numbers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 114,
Issue. 2,
p.
191.
Dubitskas, A.
1994.
On a linear form of powers of rationals.
Lithuanian Mathematical Journal,
Vol. 34,
Issue. 1,
p.
1.
Pupyrev, Yu. A.
2009.
Effectivization of a lower bound for ‖(4/3) k ‖.
Mathematical Notes,
Vol. 85,
Issue. 5-6,
p.
877.
Пупырев, Юрий Александрович
and
Pupyrev, Yuri Aleksandrovich
2009.
Рациональные приближения числа $\sqrt[3]{3}$.
Математические заметки,
Vol. 86,
Issue. 5,
p.
736.
Пупырев, Юрий Александрович
and
Pupyrev, Yuri Aleksandrovich
2009.
Эффективизация нижней оценки для $\|(4/3)^k\|$.
Математические заметки,
Vol. 85,
Issue. 6,
p.
927.
Pupyrev, Yu. A.
2009.
Rational approximations of the number % MathType!MTEF!2!1!+- % feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbbf9v8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaGcba % qaaiaaiodaaSqaaiaaiodaaaaaaa!3937! $$ \sqrt[3]{3} $$.
Mathematical Notes,
Vol. 86,
Issue. 5-6,
p.
693.
Зудилин, Вадим Валентинович
and
Zudilin, Wadim Valentinovich
2011.
Арифметические гипергеометрические ряды.
Успехи математических наук,
Vol. 66,
Issue. 2,
p.
163.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
195.
Melvyn B. Nathanson
2013.
On the Fractional Parts of Roots of Positive Real Numbers.
The American Mathematical Monthly,
Vol. 120,
Issue. 5,
p.
409.
Masser, David
2021.
Alan Baker, FRS, 1939–2018.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 6,
p.
1916.
Bugeaud, Yann
2022.
Fractional parts of powers of real algebraic numbers.
Comptes Rendus. Mathématique,
Vol. 360,
Issue. G5,
p.
459.