Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-10T11:51:57.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Flag modules and the hit problem for the Steenrod algebra

Published online by Cambridge University Press:  01 July 2009

G. WALKER  and
R. M. W. WOOD
G. WALKER
Affiliation:
School of Mathematics, The University of Manchester, Oxford Road, Manchester M13 9PL. e-mail: [email protected], [email protected]
R. M. W. WOOD
Affiliation:
School of Mathematics, The University of Manchester, Oxford Road, Manchester M13 9PL. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The ‘hit problem’ of F. P. Peterson in algebraic topology asks for a minimal generating set for the polynomial algebra P(n) = 2[x1,. . ., xn] as a module over the Steenrod algebra 2. An equivalent problem is to find an 2-basis for the subring K(n) of elements f in the dual Hopf algebra D(n), a divided power algebra, such that Sqk(f)=0 for all k > 0. The Steenrod kernel K(n) is a 2GL(n,2)-module dual to the quotient Q(n) of P(n) by the hit elements +2P(n). A submodule S(n) of K(n) is obtained as the image of a family of maps from the permutation module Fl(n) of GL(n,2) on complete flags in an n-dimensional vector space V over 2. We use the Schubert cell decomposition of the flags to calculate S(n) in degrees 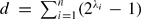, where λ1 > λ2 > ⋅⋅⋅ > λn ≥ 0. When λn = 0, we define a 2GL(n,2)-module map δ: Qd(n) → Q2d+n−1(n) analogous to the well-known isomorphism Qd(n) → Q2d+n(n) of M. Kameko. When λn−1 ≥ 2, we show that δ is surjective and δ*: S2d+n−1(n)→ Sd(n) is an isomorphism.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 147 , Issue 1 , July 2009 , pp. 143 - 171
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alghamdi, M. A., Crabb, M. C. and Hubbuck, J. R. Representations of the homology of BV and the Steenrod algebra I. In Adams Memorial Symposium on Algebraic Topology vol. 2, London Math. Soc. Lecture Note Ser. vol. 176 (Cambridge University Press, 1992), pp. 217–234.Google Scholar
[2]Boardman, J. M. Modular representations on the homology of powers of real projective spaces. In Algebraic Topology, (Oaxtepec 1991), Contemp. Math. 146 (1993), 49–70.CrossRefGoogle Scholar
[3]Carter, R. W.Representation theory of the 0-Hecke algebra. J. Algebra 104 (1986), 89–103.Google Scholar
[4]Crabb, M. C. and Hubbuck, J. R. Representations of the homology of BV and the Steenrod algebra II. In Algebraic Topology: new trends in localization and periodicity 1994 (Sant Feliu de Guixols), Progr. Math. 136 (Birkhaüser, 1996), 143–154.CrossRefGoogle Scholar
[5]Fulton, W.Young Tableaux. London Math. Soc. Stud. Texts vol. 35 (Cambridge University Press, 1997).Google Scholar
[6]Humphreys, J. E.Modular Representations of Finite Groups of Lie Type. London Math. Soc. Lecture Note Ser. vol. 326 (Cambridge University Press, 2005).CrossRefGoogle Scholar
[7]Kameko, M. Products of projective spaces as Steenrod modules. Ph.D. thesis. Johns Hopkins University (1990).Google Scholar
[8]Kameko, M.Generators of the cohomology of BV 3. J. Math. Kyoto Univ. 38 (1998), 587–593.Google Scholar
[9]Kameko, M.Generators of the cohomology of BV 4. Preprint, Toyama University (2003).Google Scholar
[10]Nam, Tran Ngoc-générateurs génériques pour l'algèbre polynomiale. Adv. Math. 186 (2004), 334–362.CrossRefGoogle Scholar
[11]Nam, Tran NgocTransfert algébrique et action du groups linéaire sur les puissances divisées, Ann. Inst. Fourier (Grenoble) 58 (2008), 1785–1837.CrossRefGoogle Scholar
[12]Norton, P. N.0-Hecke algebras. J. Aust. Math. Soc. (Ser. A) 27 (1979), 337–357.CrossRefGoogle Scholar
[13]Peterson, F. P. Generators of H*(RP ∞ ∧ RP ∞) as a module over the Steenrod algebra. Abstracts Amer. Math. Soc. (1987), 833-55-89.Google Scholar
[14]Repka, J. and Selick, P.On the subalgebra of H *((RP ∞)n; 2) annihilated by Steenrod operations. J. Pure Appl. Algebra 127 (1998), 273–288.CrossRefGoogle Scholar
[15]Singer, W. M.The transfer in homological algebra. Math. Z. 202 (1989), 493–523.Google Scholar
[16]Singer, W. M.On the action of Steenrod squares on polynomial algebras. Proc. Amer. Math. Soc. 111 (1991), 577–583.Google Scholar
[17]Sum, Nguyen The hit problem for the polynomial algebra of four variables. Preprint, Quynhon University, Vietnam (2007).Google Scholar
[18]Wood, R. M. W.Steenrod squares of polynomials and the Peterson conjecture. Math. Proc. Camb. Phil. Soc. 105 (1989), 307–309.Google Scholar
[19]Wood, R. M. W.Problems in the Steenrod algebra. Bull. London Math. Soc. 30 (1998), 194–220.CrossRefGoogle Scholar
[20]Walker, G. and Wood, R. M. W.Linking first occurrence polynomials over 2 by Steenrod operations. J. Algebra 246 (2001), 739–760.CrossRefGoogle Scholar
[21]Walker, G. and Wood, R. M. W.Weyl modules and the mod 2 Steenrod Algebra. J. Algebra 311 (2007), 840–858.CrossRefGoogle Scholar
[22]Walker, G. and Wood, R. M. W. Young tableaux and the Steenrod algebra. In Proceedings of the School and Conference in Algebraic Topology (Hanoi, 2004) Geom. Topol. Monogr. 11 (2007), 379–398.CrossRefGoogle Scholar
[23]Zara, C.Chains, subwords and fillings: strong equivalence of three definitions of the Bruhat order. Electron. J. Combin. 13 (2006), No. 1, Note 5, 13pp.Google Scholar