Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Leinen, Felix
and
Phillips, Richard E.
1987.
Group Theory.
Vol. 1281,
Issue. ,
p.
85.
Ensel, Heiner
1988.
Die Automorphismengruppe der abz�hlbaren, existentiell abgeschlossenenP A -GruppeE A.
Archiv der Mathematik,
Vol. 51,
Issue. 3,
p.
198.
Haug, Frieder
Meierfrankenfeld, Ulrich
and
Phillips, Richard E.
1991.
An amalgamation theorem for finite group extensions.
Archiv der Mathematik,
Vol. 57,
Issue. 4,
p.
325.
Leinen, Felix
1992.
Existentially closed locally cofinite groups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 35,
Issue. 2,
p.
233.
Leinen, Felix
1993.
Countable closed 𝐿𝐹𝐶-groups with 𝑝-torsion.
Transactions of the American Mathematical Society,
Vol. 336,
Issue. 1,
p.
193.
Leinen, F.
1995.
Finite and Locally Finite Groups.
p.
285.


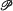 will denote the class of all locally finite
will denote the class of all locally finite