Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T08:24:05.301Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence theorems for H-space inverses

Published online by Cambridge University Press:  24 October 2008

Robin Sibson
Robin Sibson
Affiliation:
King's College, Cambridge, England
Get access Rights & Permissions [Opens in a new window]

Extract

We define an unbased H-space to be a pair (A, m) where A is a space and

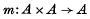
is a map such that the maps La: x → m(a, x), Ra: x → m(x, a) are homotopy equivalences for all a ∈ A. This is the same as James's definition of an H'-space in (3); we follow his notation as far as possible. (A, m) is homotopy-associative if the maps m(m × 1) and m(l × m) are homotopic. A left (right) a-inverse (a ∈ A) is a map w: A → A such that the composition m(w × 1) d (w(1 × w) d) is homotopic to ka, the constant map to a. d denotes the diagonal map a → (a, a).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 1 , January 1969 , pp. 19 - 21
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Dold, A.Partitions of unity in the theory of fibrations. Ann. of Math. 78 (1963), 223–255.Google Scholar
(2)James, I. M.On H-spaces and their homotopy groups. Quart. J. Math. Oxford Ser. 2, 11 (1960), 161–179.Google Scholar
(3)James, I. M.Quasigroups and topology. Math. Z. 84 (1964), 329–342.Google Scholar
(4)Milnor, J. W.Spaces having the homotopy type of a CW-complex. Trans. Amer. Math. Soc. 90 (1959), 272–280.Google Scholar
(5)Sugawara, Masahiro. On a condition that a space is an H-space. Math. J. Okayama Univ. 6 (1957), 109–128.Google Scholar
(6)Whitehead, G. W.Note on a theorem of Sugawara. Bol. Soc. Mat. Mexicana 4 (1959), 33–41.Google Scholar