Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T05:06:29.321Z Has data issue: false hasContentIssue false
  • English
  • Français

The Electrical Resistance of Dilute Solid Solutions

Published online by Cambridge University Press:  24 October 2008

N. F. Mott
N. F. Mott
Affiliation:
Professor of Theoretical Physics, University of Bristol
Get access Rights & Permissions [Opens in a new window]

Extract

1. As is well known, the electrical resistance of a metal is very greatly in-creased by the addition of a second metal with which it forms a solid solution. The increase Δρ in the resistivity due to the addition of a small percentage of the second metal is in general independent of the temperature (Matthiessen's rule), though there are oertain exceptions (e.g. Cr in Au). The quaritum-mechanical explanation of both these facts was first given by Nordheim, and may be expressed as follows: the electrical conductivity of any metal may be written in the form

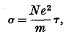
where τ is the “time of relaxation”, equal to half the time between collisions, and N is the effective number of free electrons per unit volume: hence, for the resistivity, we have

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 32 , Issue 2 , May 1936 , pp. 281 - 290
Copyright
Copyright © Cambridge Philosophical Society 1936

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

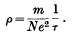
† Ann. d. Phya. (5), 9 (1931), 607.Google Scholar

† Zeits. f. Phys. 45 (1927), 307. Cf. also Mott and Massey, The theory of atomic collisions, Ch. II.CrossRefGoogle Scholar

‡ Phys. Rev. 43 (1933), 804.CrossRefGoogle Scholar

† Cf., for instance, Sommerfeld, and Bethe, , Handb. d. Phys. 24/2 (1933), 548et seq.Google Scholar

‡ Cf. Mott, and Massey, , loc. cit. p. 230.Google Scholar

† Cf. Mott, and Massey, loc. cit. Ch. II.Google Scholar

‡ Loc. cit. Ch. VII.

† Cf. Sommerfeld, and Bethe, , loc. cit., and Zener, Nature, 132 (1933), 968.Google Scholar

‡ Ann. d. Phys. 15 (1932), 219.Google Scholar

§ Meier, , Ann. d. Phys. 31 (1910), 1017.CrossRefGoogle Scholar

║ Forsterling, and Freederichsz, Ann. d. Phys. 40 (1913), 201.CrossRefGoogle Scholar

Hagen, and Rubens, , Ann. d. Phys. 40 (1913), 201.Google Scholar

** Mott, and Zener, , Proc. Camb. Phil. Soc. 30 (1934), 249. Cf. the table on p. 262.CrossRefGoogle Scholar

‡‡ Proc. Roy. Soc. A, 151 (1935), 585.CrossRefGoogle Scholar

† Cf. Mott, , Proc. Phys. Soc. 46 (1934), 680, for other examples of the same kind.CrossRefGoogle Scholar

‡ Fuchs, , Proc. Roy. Soc. A, 151 (1935), 585.CrossRefGoogle Scholar

§ Unpublished; I wish to thank Miss Littleton for carrying out the calculations, and Prof. Hartree for providing us with the field before publication.

‖ Loc. cit.

† Proc. Roy. Soc. A, 141 (1930), 225.Google Scholar

† Loc. cit.

‡ Proc. Camb. Phil. Soc. 23 (1927), 542.CrossRefGoogle Scholar

§ Zeits. f. Phys. 48 (1928), 73.CrossRefGoogle Scholar

† Cf. Wentzel, , Zeits. J. Phys. 40 (1927), 590.CrossRefGoogle Scholar