Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T14:29:42.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective mean value estimates for complex multiplicative functions

Published online by Cambridge University Press:  24 October 2008

R. R. Hall  and
G. Tenenbaum
R. R. Hall
Affiliation:
Department of Mathematics, York University, Heslington, York YOl 5DD
G. Tenenbaum
Affiliation:
Département de Mathématiques, Université de Nancy I, BP 239, 54506 Vandœuvre Cedex, France
Get access Rights & Permissions [Opens in a new window]

Extract

Quantitative estimates for finite mean values

of multiplicative functions are highly applicable tools in analytic and probabilistic number theory. Extending a result of Hall [4], Halberstam and Richert[3] proved a useful inequality valid for real, non-negative g satisfying for instance a Wirsing type condition, viz 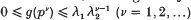for all primes p, with constants λ1 ≥ 0, 0 ≤ λ2 < 2. Their upper bound is sharp to within a factor (l + o(l)), but even a weaker and easier to prove estimate, such as

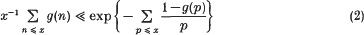
(where the implied constants depend on λ1 and λ2), may become a surprisingly strong device. For instance, setting g(p) = l ± ε, where ε is an arbitrarily small positive number, provides immediately a proof of the famous Hardy–Ramanujan theorem on the normal order of the number of prime factors of an integer. This example, and many others, are discussed in detail in our book [5] where we make extensive use of (2) for various problems connected with the structure of the set of divisors of a normal number.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 2 , September 1991 , pp. 337 - 351
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Elliott, P. D. T. A.. Some remarks about multiplicative functions of modulus ≤ 1. In Analytic Number Theory (eds. Berndt, B. C., Diamond, H. G., Halberstam, H., Hildebrand, A.), Progress in Math. no. 85 (Birkhäuser, 1990), pp. 159–164.CrossRefGoogle Scholar
[2]Halász, G.. On the distribution of additive and the mean value of multiplicative arithmetic functions. Studia Sci. Math. Hungar. 6 (1971), 211–233Google Scholar
[3]Halberstam, H. and Richert, H.-E.. On a result of R. R. Hall. J. Number Theory (1) 11 (1979), 76–89.CrossRefGoogle Scholar
[4]Hall, R. R.. Halving an estimate obtained from Selberg's upper bound method. Acta Arith. 25 (1974), 347–351.Google Scholar
[5]Hall, R. R. and Tenenbaum, G.. Divisors. Cambridge Tracts in Mathematics no. 90 (Cambridge University Press, 1988).Google Scholar
[6]Hildebrand, A.. Quantitative mean-value theorems for non-negative multiplicative functions 1. J. London Math. Soc. (2) 30 (1984), 394–406.CrossRefGoogle Scholar
[7]Heldebrand, A.. Quantitative mean-value theorems for non-negative multiplicative functions 2. Acta Arith. 48 (1987), 209–260.CrossRefGoogle Scholar
[8]Maier, H. and Tenenbaum, G.. On the set of divisors of an integer. Invent. Math. 76 (1984), 121–128.CrossRefGoogle Scholar
[9]Montgomery, H. L., A note on the mean values of multiplicative functions. Inst. Mittag Leffler, report No. 17 (1978).Google Scholar
[10]Tenenbaum, G.. Introduction à la Théorie Analytique et Probabiliste des Nombres (Institut Elie Cartan, Nancy, 1990).Google Scholar