Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T13:39:33.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuous data dependence for the equations of classical elastodynamics†

Published online by Cambridge University Press:  24 October 2008

R. J. Knops  and
L. E. Payne
R. J. Knops
Affiliation:
University of Newcastle; Cornell University
L. E. Payne
Affiliation:
University of Newcastle; Cornell University
Get access Rights & Permissions [Opens in a new window]

Extract

Consider a linear elastic solid occupying a bounded regular three-dimensional region B with smooth surface ∂B. The components of displacement ui referred to cartesian axes xi are then well known to satisfy the system of governing equations

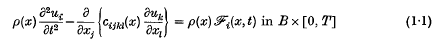
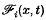in which t denotes the time variable, x = (x1, x2, x3) denotes the position vector, ρ(x) is the non-homogeneous density, assumed positive,. i(x, t) are the Cartesian components of body force per unit mass, and cijkl(x) are the non-homogeneous elasticities, which apart from certain smoothness conditions stated later, are assumed to possess the symmetry

Throughout this paper, all suffixes range over the values 1, 2, 3 and the usual converition of summing over repeated indices is adopted. Except where it is in the interest of clarity we avoid explicit mention of the dependence of functions on their arguments.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 2 , September 1969 , pp. 481 - 491
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bramble, J. H. and Hubbard, B. E.Some higher order integral identities with applications to boundary techniques. Nat. Bur. Standards Sect. B 65 (1961), 269–276.CrossRefGoogle Scholar
(2)Bramble, J. H. and Payne, L. E.Effect of error in measurement of elastic constants on the solutions of problems in classical elasticity. Nat. Bur. Standards Sect. B 67 (1963), 157–167.CrossRefGoogle Scholar
(3)Gurtin, M. E. and Sternberg, E.A note on uniqueness in classical elastodynamics. Quart. Appl. Math. 19 (1961), 169–171.CrossRefGoogle Scholar
(4)Gurtin, M. E. and Toupin, R. A.A uniqueness theorem for the displacement boundary-value problem of linear elastodynamics. Quart. Appl. Math. 23 (1965), 79–81.CrossRefGoogle Scholar
(5)Hayes, M. and Knops, R. J.On the displacement boundary value problem of linear elastodynamics. Quart. Appl. Math. 25 (1968), 291–293.CrossRefGoogle Scholar
(6)Holden, J. T.Estimation of critical loads in elastic stability theory. Arch. Rational Mech. Anal. 17 (1964), 171–183.CrossRefGoogle Scholar
(7)Knops, R. J. and Payne, L. E.Uniqueness in classical elastodynamics. Arch. Rational Mech. Anal. 27 (1968), 349–355.CrossRefGoogle Scholar
(8)Knops, R. J. and Payne, L. E.Stability in linear elasticity. Internat. J. Sols. Structs. 4 (1968), 1233–1242.CrossRefGoogle Scholar
(9)Knops, R. J. and Payne, L. E.Stability of the traction boundary value problem in linear elastodynamics. Internat. J. Engng Sci. 6 (1968), 351–357.CrossRefGoogle Scholar
(10)Movchan, A. A.On the stability of processes in the deformation of continuous bodies. Arch. Mech. Stos. 15 (1963), 659.Google Scholar
(11)Neumann, F. Vorlesungen über die Theorie der Elasticität der fester Körper und das Lichtather B. G. Teubner, Leipzig (1885).Google Scholar
(12)Payne, L. E. On some non-well posed problems for partial differential equations. Numerical solutions of non-linear differential equations. (John Wiley and Sons, inc., 1964.)Google Scholar
(13)Shield, R. T.On the stability of linear continuous systems. Z. Angew Math. Phys. 16 (1965), 649–686.CrossRefGoogle Scholar
(14)Sigillito, V.A priori inequalities and pointwise bounds for solutions of fourth order elliptic partial differential equations. SIAM. J. Appl. Math. 15 (1967), 1136–1155.Google Scholar
(15)Wilcox, C.Initial-boundary value problems for linear hyperbolic, partial differential equations of the second order. Arch. Rational Mech. Anal. 10 (1962), 361–400.CrossRefGoogle Scholar