No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
The initial collision (see pp. 571–2). The instantaneous velocity change of the hammer (from V0 to V) when it first strikes the liquid film should be calculated from energy and not momentum considerations, since the hammer has momentum in the vertical direction whilst the liquid is expressed in a horizontal direction and its total momentum is, by symmetry, zero at every instant. The kinetic energy dE of an annulus of liquid of radius r will be ½mc2, where m = 2πrhρdr, and c, the radial velocity of flow, is ½rV/h, since the liquid starts moving in plug flow. Integrating from r = 0 to r = R, we find that the total kinetic energy E imparted to the liquid film is 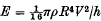 . Assuming that extraneous energy losses, including any energy imparted to the anvil, are negligible, we may equate this to the energy loss of the hammer
. Assuming that extraneous energy losses, including any energy imparted to the anvil, are negligible, we may equate this to the energy loss of the hammer 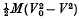 . Hence
. Hence
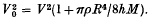
To a first approximation this yields

The term at the right-hand side of the denominator is one-half that given in the original derivation (equation (20)), so that the instantaneous decrease in the velocity of the hammer is even less marked. For the given case where M = 400g., R = 1 cm., ρ = 1.6 and h = 5 × 10−2 cm., the velocity decrease is less than 2%.
Vol. 44 (1948), pp. 566–80.