Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huneke, Craig L.
and
Sharp, Rodney Y.
1993.
Bass numbers of local cohomology modules.
Transactions of the American Mathematical Society,
Vol. 339,
Issue. 2,
p.
765.
Lyubeznik, Gennady
1993.
Finiteness properties of local cohomology modules (an application ofD-modules to commutative algebra).
Inventiones Mathematicae,
Vol. 113,
Issue. 1,
p.
41.
Delfino, Donatella
1994.
On the cofiniteness of local cohomology modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 1,
p.
79.
Kawasaki, Ken-ichiroh
1996.
On the finiteness of Bass numbers of local cohomology modules.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 11,
p.
3275.
Belshoff, Richard
Slattery, Susan
and
Wickham, Cameron
1996.
The local cohomology modules of Matlis reflexive modules are almost cofinite.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 9,
p.
2649.
Yoshida, Ken-Ichi
1997.
Cofiniteness of local cohomology modules for ideals of dimension one.
Nagoya Mathematical Journal,
Vol. 147,
Issue. ,
p.
179.
Koh, Jee
and
Lee, Kisuk
1998.
Some Restrictions on the Maps in Minimal Resolutions.
Journal of Algebra,
Vol. 202,
Issue. 2,
p.
671.
Hellus, M
2001.
On the Set of Associated Primes of a Local Cohomology Module.
Journal of Algebra,
Vol. 237,
Issue. 1,
p.
406.
Yassemi, Siamak
2001.
COFINITE MODULES.
Communications in Algebra,
Vol. 29,
Issue. 6,
p.
2333.
Khashyarmanesh, K.
and
Salarian, Sh.
2002.
A FINITENESS RESULT FOR LOCAL COHOMOLOGY MODULES.
Communications in Algebra,
Vol. 30,
Issue. 10,
p.
4821.
Asadollahi, J.
Khashyarmanesh, K.
and
Salarian, Sh.
2002.
ON THE FINITENESS PROPERTIES OF THE GENERALIZED LOCAL COHOMOLOGY MODULES.
Communications in Algebra,
Vol. 30,
Issue. 2,
p.
859.
Marley, Thomas
and
Vassilev, Janet C.
2002.
Cofiniteness and associated primes of local cohomology modules.
Journal of Algebra,
Vol. 256,
Issue. 1,
p.
180.
ASADOLLAHI, J.
and
SCHENZEL, P.
2003.
Some results on associated primes of local cohomology modules.
Japanese journal of mathematics. New series,
Vol. 29,
Issue. 2,
p.
285.
Asadollahi, J.
Khashyarmanesh, K.
and
Salarian, SH.
2003.
A generalization of the cofiniteness problem in local cohomology modules.
Journal of the Australian Mathematical Society,
Vol. 75,
Issue. 3,
p.
313.
Melkersson, Leif
2005.
Modules cofinite with respect to an ideal.
Journal of Algebra,
Vol. 285,
Issue. 2,
p.
649.
Dibaei, Mohammad T.
and
Yassemi, Siamak
2006.
Finiteness of Extension Functors of Local Cohomology Modules.
Communications in Algebra,
Vol. 34,
Issue. 8,
p.
3097.
Khashyarmanesh, Kazem
2006.
On the finiteness properties of extension and torsion functors of local cohomology modules.
Proceedings of the American Mathematical Society,
Vol. 135,
Issue. 5,
p.
1319.
Khashyarmanesh, K.
and
Khosh-Ahang, F.
2008.
On the Local Cohomology of Matlis Reflexive Modules.
Communications in Algebra,
Vol. 36,
Issue. 2,
p.
665.
Sabzrou, Hossein
and
Tousi, Massoud
2008.
Local Cohomology at Monomial Ideals inR-Sequences.
Communications in Algebra,
Vol. 36,
Issue. 1,
p.
37.
Nam, Tran Tuan
2008.
Co-support and Coartinian Modules.
Algebra Colloquium,
Vol. 15,
Issue. 01,
p.
83.


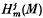 are known to be Artinian. Grothendieck [3], exposé 13, 1·2 made the following conjecture:
are known to be Artinian. Grothendieck [3], exposé 13, 1·2 made the following conjecture: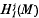 ) is finitely generated.
) is finitely generated.