Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T14:16:45.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Chebyshev’s bias for analytic L-functions

Part of: Arithmetic algebraic geometry Multiplicative number theory Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  22 March 2019

LUCILE DEVIN
LUCILE DEVIN*
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 150 Louis Pasteur pvt, Ottawa, Ontario K1N 6N5, Canada. email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We discuss the generalizations of the concept of Chebyshev’s bias from two perspectives. First, we give a general framework for the study of prime number races and Chebyshev’s bias attached to general L-functions satisfying natural analytic hypotheses. This extends the cases previously considered by several authors and involving, among others, Dirichlet L-functions and Hasse–Weil L-functions of elliptic curves over Q. This also applies to new Chebyshev’s bias phenomena that were beyond the reach of the previously known cases. In addition, we weaken the required hypotheses such as GRH or linear independence properties of zeros of L-functions. In particular, we establish the existence of the logarithmic density of the set 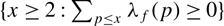$ \{x \ge 2:\sum\nolimits_{p \le x} {\lambda _f}(p) \ge 0\}$ for coefficients (λf(p)) of general L-functions conditionally on a much weaker hypothesis than was previously known.

MSC classification

Primary: 11N45: Asymptotic results on counting functions for algebraic and topological structures 11F30: Fourier coefficients of automorphic forms 11S40: Zeta functions and $L$-functions
Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 1 , July 2020 , pp. 103 - 140
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akbary, A., Ng, N. and Shahabi, M.. Limiting distributions of the classical error terms of prime number theory. Q. J. Math. 65 (2014), no. 3, 743–780.CrossRefGoogle Scholar
Bass, R. F.. Probabilistic techniques in analysis. Probability and its Applications (New York), (Springer–Verlag, New York, 1995).Google Scholar
Breuil, C., Conrad, B., Diamond, F. and Taylor, R.. On the modularity of elliptic curves over Q: wild 3-adic exercises. J. Amer. Math. Soc. 14 (2001), no. 4, 843–939.CrossRefGoogle Scholar
Bump, D. and Friedberg, S.. The exterior square automorphic L-functions on GL(n). Festschrift in honor of I. I. Piatetski–Shapiro on the occasion of his sixtieth birthday, Part II (Ramat Aviv, 1989), Israel Math. Conf. Proc., vol. 3 (Weizmann, Jerusalem, 1990), pp. 47–65.Google Scholar
Bump, D. and Ginzburg, D.. Symmetric square L-functions on GL(r). Ann. of Math. (2) 136 (1992), no. 1, 137–205.CrossRefGoogle Scholar
Bourbaki, N.. Éléments de mathématique. Première partie: Les structures fondamentales de l’analyse. Livre III: Topologie générale. Chapitre V: Groupes à un paramètre. Chapitre VI: Espace numériques et espaces projectifs. Chapitre VII: Les groupes additifs Rn. Chapitre VIII: Nombres complexes. Actualités Sci. Ind., no. 1029, (Hermann et Cie., Paris, 1947).Google Scholar
Clozel, L., Harris, M. and Taylor, R.. Automorphy for some l-adic lifts of automorphic mod l Galois representations. Publ. Math. Inst. Hautes Études Sci. (2008), no. 108, 1–181. With Appendix A, summarising unpublished work of Russ Mann, and Appendix B by Marie–France Vignéras.CrossRefGoogle Scholar
Cogdell, J. W.. Lectures on L-functions, converse theorems and functoriality for GLn, Lectures on automorphic L-functions. Fields Inst. Monogr., vol. 20, (Amer. Math. Soc., Providence, RI, 2004), pp. 1–96.Google Scholar
Conrad, K.. Partial Euler products on the critical line. Canad. J. Math. 57 (2005), no. 2, 267–297.CrossRefGoogle Scholar
Cogdell, J. W. and Piatetski–Shapiro, I. I.. Remarks on Rankin–Selberg Convolutions, Contributions to automorphic forms, geometry, and number theory. (University Johns Hopkins Univ. Press, Baltimore, MD, 2004), pp. 255–278.Google Scholar
Deligne, P.. La conjecture de Weil. I. Inst. Hautes Études Sci. Publ. Math. (1974), no. 43, 273–307.CrossRefGoogle Scholar
Devin, L.. Propriétés algébriques et analytiques de certaines suites indexées par les nombres premiers. PhD. thesis. Université Paris-Sud 11, Université Paris–Saclay, (2017).Google Scholar
Deligne, P. and Serre, J.–P.. Formes modulaires de poids 1. Ann. Sci. École Norm. Sup. (4) 7 (1974), 507–530 (1975).CrossRefGoogle Scholar
Fiorilli, D.. Elliptic curves of unbounded rank and Chebyshev’s bias. Int. Math. Res. Not. IMRN (2014), no. 18, 4997–5024.CrossRefGoogle Scholar
Fiorilli, D.. Highly biased prime number races. Algebra Number Theory 8 (2014), no. 7, 1733–1767.CrossRefGoogle Scholar
Ford, K. and Konyagin, S.. Chebyshev’s conjecture and the prime number race, IV International Conference “Modern Problems of Number Theory and its Applications”: Current Problems, Part II (Russian) (Tula, 2001). Mosk. Gos. Univ. im. Lomonosova, Mekh.-Mat. Fak., (Moscow, 2002), pp. 67–91.Google Scholar
Fiorilli, D. and Martin, G.. Inequities in the Shanks-Rényi prime number race: an asymptotic formula for the densities. J. Reine Angew. Math. 676 (2013), 121–212.Google Scholar
Godement, R. and Jacquet, H.. Zeta functions of simple algebras. Lecture Notes in Math. vol. 260. (Springer-Verlag, Berlin-New York, 1972).Google Scholar
Granville, A. and Martin, G.. Prime number races. Amer. Math. Monthly 113 (2006), no. 1, 1–33.CrossRefGoogle Scholar
Goldfeld, D.. Sur les produits partiels eulériens attachés aux courbes elliptiques. C. R. Acad. Sci. Paris Sér. I Math. 294 (1982), no. 14, 471–474.Google Scholar
Harris, M.. Potential automorphy of odd-dimensional symmetric powers of elliptic curves and applications. Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. II, Progr. Math., vol. 270. (Birkhäuser Boston, Inc., Boston, MA, 2009), pp. 1–21.Google Scholar
Harris, M., Shepherd–Barron, N. and Taylor, R.. A family of Calabi-Yau varieties and potential automorphy. Ann. of Math. (2) 171 (2010), no. 2, 779–813.CrossRefGoogle Scholar
Humphries, P.. The summatory function of Liouville’s function and Pólya’s conjecture. (October 2010).Google Scholar
Iwaniec, H. and Kowalski, E.. Analytic number theory. American Mathematical Society Colloquium Publications, vol. 53. (American Mathematical Society, Providence, RI, 2004).Google Scholar
Jacquet, H. and Shalika, J.. Exterior square L-functions. Automorphic forms, Shimura varieties and L-functions, Vol. II (Ann Arbor, MI, 1988), Perspect. Math., vol. 11 (Academic Press, Boston, MA, 1990), pp. 143–226.Google Scholar
Kaczorowski, J.. On the distribution of primes (mod 4). Analysis 15 (1995), no. 2, 159–171.CrossRefGoogle Scholar
Katznelson, Y.. An introduction to harmonic analysis, third ed. (Cambridge Mathematical Library, Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Kowalski, E. and Michel, P.. Explicit upper bound for the (analytic) rank of J 0(q). Israel J. Math. 120 (2000), no. part A, 179–204.CrossRefGoogle Scholar
Kowalski, E.. A lower bound for the rank of J 0(q). Acta Arith. 94 (2000), no. 4, 303–343.CrossRefGoogle Scholar
Kaczorowski, J. and Perelli, A.. On the prime number theorem for the Selberg class. Archiv der Mathematik 80 (2003), no. 3, 255–263.Google Scholar
Kaczorowski, J. and Ramaré, O.. Almost periodicity of some error terms in prime number theory. Acta Arith. 106 (2003), no. 3, 277–297.CrossRefGoogle Scholar
Lang, S.. Algebra, third ed. Graduate Texts in Math. vol. 211 (Springer-Verlag, New York, 2002).CrossRefGoogle Scholar
Mazur, B.. Finding meaning in error terms. Bull. Amer. Math. Soc. (N.S.) 45 (2008), no. 2, 185–228.CrossRefGoogle Scholar
Martin, G. and Ng, N.. Inclusive prime number races. arXiv:1710.00088. (Oct. 2017).Google Scholar
Montgomery, H. L. and Vaughan, R. C.. Multiplicative number theory. I. Classical theory. Camb. Stud. Adv. Math., vol. 97. (Cambridge University Press, Cambridge, 2007).Google Scholar
Mœglin, C. and Waldspurger, J.–L.. Le spectre résiduel de GL(n). Ann. Sci. École Norm. Sup. (4) 22 (1989), no. 4, 605–674.CrossRefGoogle Scholar
Ng, N.. Limiting distributions and zeros of Artin L-functions. PhD. thesis University of British Colombia. (2000).Google Scholar
Ramakrishnan, D.. Modularity of the Rankin-Selberg L-series, and multiplicity one for SL(2). Ann. of Math. (2) 152 (2000), no. 1, 45–111.CrossRefGoogle Scholar
Rubinstein, M. and Sarnak, P.. Chebyshev’s bias. Experiment. Math. 3 (1994), no. 3, 173–197.CrossRefGoogle Scholar
Rudin, W.. Analyse Réelle et Complexe. (Masson, Paris, 1980). Translated from the first English edition by Dhombres, N. and Hoffman, F., Third printing.Google Scholar
Rudin, W.. Fourier analysis on groups. (Wiley Classics Library, John Wiley & Sons, Inc., New York, 1990). Reprint of the 1962 original, a Wiley-Interscience Publication.CrossRefGoogle Scholar
Ramakrishnan, D. and Valenza, R. J.. Fourier analysis on number fields. Graduate Texts in Mathematics. vol. 186. (Springer-Verlag, New York, 1999).Google Scholar
Sagemath, the Sage Mathematics Software System (Version 7.3). (2016), http://www.sagemath.org.Google Scholar
Sarnak, P.. Letter to: Barry Mazur on “Chebychev’s bias” for τ(p). Publications.ias. (2007), URL: https://publications.ias.edu/sites/default/files/MazurLtrMay08.PDF (version: 2008-05).Google Scholar
Stienstra, J. and Beukers, F.. On the Picard-Fuchs equation and the formal Brauer group of certain elliptic K3-surfaces. Math. Ann. 271 (1985), no. 2, 269–304.CrossRefGoogle Scholar
Schoeneberg, B.. Über den Zusammenhang der Eisensteinschen Reihen und Thetareihen mit der Diskriminante der elliptischen Funktionen. Math. Ann. 126 (1953), 177–184.CrossRefGoogle Scholar
Shahidi, F.. On non-vanishing of twisted symmetric and exterior square L-functions for GL(n). Pacific J. Math. (1997), no. Special Issue, 311–322, Olga Taussky-Todd: in memoriam.CrossRefGoogle Scholar
Shimura, G.. Introduction to the arithmetic theory of automorphic functions. Publications of the Mathematical Society of Japan, vol. 11. (Princeton University Press, Princeton, NJ, 1994). Reprint of the 1971 original, Kanô Memorial Lectures, 1.Google Scholar
Stein, E. M.. Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, vol. 43. (Princeton University Press, Princeton, NJ, 1993). With the assistance of Timothy S. Murphy, Monographs in Harmonic Analysis, III.Google Scholar
Taylor, R. and Wiles, A.. Ring-theoretic properties of certain Hecke algebras. Ann. of Math. (2) 141 (1995), no. 3, 553–572.CrossRefGoogle Scholar
Watson, G. N.. A treatise on the theory of Bessel functions. (Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1995). Reprint of the second (1944) edition.Google Scholar
Wiles, A.. Modular elliptic curves and Fermat’s last theorem. Ann. of Math. (2) 141 (1995), no. 3, 443–551.CrossRefGoogle Scholar
Wintner, A.. On the distribution function of the remainder term of the prime number theorem. Amer. J. Math. 63 (1941), 233–248.CrossRefGoogle Scholar