Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T17:17:45.370Z Has data issue: false hasContentIssue false
  • English
  • Français

Characteristic classes of Galois representations

Published online by Cambridge University Press:  24 October 2008

A. Kozlowski
A. Kozlowski
Affiliation:
Department of Mathematics, Wayne State University, Detroit, MI 48202, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let K be a field with char if K≠2 and let Ks denote the separable closure of K and GK the Galois group of the extension Ks/K. If K⊂L is a finite extension and ρ:GL↦Or(R) a (continuous) real representation of GL we have a map ρ:BGL→BO which is used to define Stiefel–Whitney classes wi(ρ) = ρ*(wi). In general if f is any element of H*(BO; ℤ/2) we denote by f(ρ) the characteristic class ρ*(f). Now let

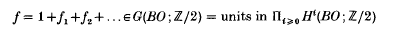
be a genus (see e.g. [9]), for example the total Stiefel–Whitney class w = 1+w1+w2 + … Let K⊂L and ρ be as above and let denote the multiplicative transfer (see e.g. [3, 5, 2, 14, 15]). Our principal result is a generalization of theorem 1 of [3]

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 108 , Issue 3 , November 1990 , pp. 517 - 522
Copyright
Copyright © Cambridge Philosophical Society 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F. and Hirzebrtjch, F.. Cohomologie-Operationen und Charakteristische Klassen. Math. Z. 77 (1961), 149–187.CrossRefGoogle Scholar
[2]Fulton, W. and MacPherson, R.. Characteristic classes of direct image bundles for covering maps. Ann. of Math. (2) 125 (1987), 1–92.CrossRefGoogle Scholar
[3]Kahn, B.. Classes de Stiefel–Whitney de formes quadratiques et représentations Galoisiennes réelles. Invent. Math. 78 (1984), 223–256.CrossRefGoogle Scholar
[4]Kahn, D. S. and Priddy, B. S.. The transfer and stable homotopy theory. Math. Proc. Cambridge Philos. Soc. 83 (1978), 103–111.CrossRefGoogle Scholar
[5]Kozlowski, A.. The transfer in Segals cohomology. Illinois J. Math. 27 (1983), 614–623.CrossRefGoogle Scholar
[6]Kozlowski, A.. Operations in Segal's cohomology. Math. Proc. Cambridge Philos. Soc. 95 (1984), 437–441.CrossRefGoogle Scholar
[7]Kozlowski, A.. The Evens–Kahn formula for the total Stiefel–Whitney class. Proc. Amer. Math. Soc. 91 (1984), 309–314.CrossRefGoogle Scholar
[8]Kozlowski, A.. Transfers in the group of multiplicative units of the classical cohomology ring and Stiefel–Whitney classes. Publ. Res. Inst. Math. Sci. 25 (1989), 54–74.CrossRefGoogle Scholar
[9]Madsen, I. and Milgram, R. J.. The Classifying Spaces for Surgery and Cobordism of Manifolds (Princeton University Press, 1979).Google Scholar
[10]Merkurjev, A. S.. On the norm residue of degree 2. Soviet Math. Dokl. 24 (1981), 546–551.Google Scholar
[11]Milnor, J. W.. Algebraic K-theory and quadratic forms. Invent. Math. 9 (1969/1970), 318–344.CrossRefGoogle Scholar
[12]Segal, G. B.. The multiplicative group of classical cohomology. Math. Z. (2) 26 (1975), 289–293.Google Scholar
[13]Serre, J-P.. L'invariant de Witt de la forme Tr x 2. Comment. Math. Helv. 59 (1984), 651–676.CrossRefGoogle Scholar
[14]Snaith, V. P.. TopologicalMethods in Galois Representation Theory (John Wiley & Sons, 1989).Google Scholar
[15]Steiner, R.. Multiplicative transfers in classical cohomology. Proc. Edinburgh Math. Soc. 25 (1982), 113–131.CrossRefGoogle Scholar