Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mcfall, J.D.
1979.
Elementary divisors of transformations related to tensor powers.
Linear and Multilinear Algebra,
Vol. 7,
Issue. 1,
p.
13.
Merris, Russell
and
Watkins, William
1981.
Elementary divisors of induced transformations on symmetry classes of tensors.
Linear Algebra and its Applications,
Vol. 38,
Issue. ,
p.
17.
Dias da Silva, J.A.
1981.
Irreducible representations of the full linear group.
Linear Algebra and its Applications,
Vol. 40,
Issue. ,
p.
161.
Hunter, D. B.
1983.
The construction of irreducible normalized representations of the general linear group.
Linear and Multilinear Algebra,
Vol. 13,
Issue. 4,
p.
357.
Hunter, D. B.
1986.
The kernels of irreducible representations of the general linear group.
Linear and Multilinear Algebra,
Vol. 20,
Issue. 1,
p.
17.
Grabmeier, Johannes
and
Kerber, Adalbert
1987.
The evaluation of irreducible polynomial representations of the general linear groups and of the unitary groups over fields of characteristic 0.
Acta Applicandae Mathematicae,
Vol. 8,
Issue. 3,
p.
271.
Dias Da Silva, J. A.
1990.
On the minimal polynomial of the associated transformation.
Linear and Multilinear Algebra,
Vol. 27,
Issue. 4,
p.
275.
Hou, Xiang-Dong
2003.
Elementary divisors of tensor products and p-ranks of binomial matrices.
Linear Algebra and its Applications,
Vol. 374,
Issue. ,
p.
255.


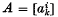 of order
of order 