Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T14:23:16.439Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bose-Einstein statistics of particles, with special reference to the case of low temperatures

Published online by Cambridge University Press:  24 October 2008

R. B. Dingle
R. B. Dingle
Affiliation:
Royal Society Mond LaboratoryCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, it has been shown that the usual demonstrations of the phenomenon of Bose-Einstein condensation are invalid. Exact formal solutions have been derived for the partition functions and the mean occupation numbers in classical and Bose statistics, and the theory of fluctuations in the case of Bose statistics has been given.

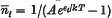In a second paper, convenient approximations will be derived for the mean occupation numbers in Bose statistics, and it will be shown that for temperatures well above the critical temperature of the supposed Bose-Einstein condensation the well-known result for the mean occupation numbers is valid, whilst for temperatures rather lower than this critical value it will be shown that particles will condense into the lowest available state. The critical temperature T0 is given by 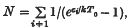where the summation is over all energy levels except the lowest.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 2 , April 1949 , pp. 275 - 287
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Sommerfeld, A.Ber. dtsch. chem. Ges. 75, no. 12 (1941), 1988.CrossRefGoogle Scholar
Gentile, G.Nuovo Cimento, 17 (1940), 493.CrossRefGoogle Scholar
(2)Schubert, G.Z. Naturforsch. 1 (3) (1946), 113 and 2 (5) (1947), 250.CrossRefGoogle Scholar
(3)London, F.Phys. Rev. 54 (1938), 947.CrossRefGoogle Scholar
(4)Fowler, R. H. and Jones, H.Proc. Cambridge Phil. Soc. 34 (1938), 573.CrossRefGoogle Scholar
(5)Fowler, R. H.Statistical Mechanics (Cambridge, 1936).Google Scholar
(6)Schrödinger, E.Statistical Thermodynamics (Cambridge, 1946). Phys. Z. 27 (1926), 95.Google Scholar
(7)Liebfried, G.Z. Naturforsch.. 2 a (6) (1947), 1.Google Scholar