Let T be an operator on a complex Banach space such that sup {‖Tn‖: n ≥ 0} < ∞; such operators are said to be power-bounded. For such an operator one defines the peripheral spectrum to be the set

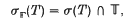
where σ(T) denotes the spectrum of T, and T is the unit circle in ℂ. Esterle proved in [3] that limnn→∞ ‖Tn−Tn+1‖ = 0 provided that ‖T‖ ≤ 1 and σ{T} = {1}. Later Katznelson and Tzafriri [6] proved the same result for power-bounded operators such that σΓ(T) = {1}, and in fact they proved a more general result. More precisely, let 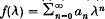be an absolutely convergent Taylor series, i.e. , and assume that f is of spectral synthesis for σΓ(T) (in particular f|σΓ(T) ≡ 0). Then limn→∞ ‖f(T) Tn‖ = 0. Katznelson and Tzafriri prove an analogous result, in which T is replaced by a commuting k-tuple (T1, T2, …, Tk) of contractions. In this case they consider functions of the form f(T1, T2, …, Tk), where f is either an absolutely convergent Taylor series if k is odd, or an element of a smaller algebra if k is even. The result of Katznelson and Tzafriri was further extended in the case of a single contraction T by Esterle, Strouse and Zouakia[4], who consider functions f(T) where f is allowed to be in a more general function algebra. For instance, if T acts on a Hilbert space, they allow f to be an element of the disk algebra.