Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-19T09:21:35.101Z Has data issue: false hasContentIssue false
  • English
  • Français

Arcs with increasing chords

Published online by Cambridge University Press:  24 October 2008

D. G. Larman  and
P. McMullen
D. G. Larman
Affiliation:
University College London, Gower Street, London WC1E 6BT
P. McMullen
Affiliation:
University College London, Gower Street, London WC1E 6BT
Get access Rights & Permissions [Opens in a new window]

Extract

Let f:[0, 1]→R2 be a Jordan arc, and for t, u ∈ [0, 1] let d(t, u) = d(f(t), f(u)) denote the Euclidean length of the chord between f(t) and f(u), and l(t, u) = l(f(t), f(u)) the corresponding arc-length, when this is defined. We say that f has the increasing chord property if d(t2, t3) ≤ d(t1, t4) whenever 0 ≤ t1 ≤ t2 ≤ t3 ≤ t4 ≤ 1. In connexion with a problem in complex analysis, K. Binmore has asked (private communication, see (1)) whether there exists an absolute constant K such that

.

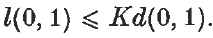Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 72 , Issue 2 , September 1972 , pp. 205 - 207
Copyright
Copyright © Cambridge Philosophical Society 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Binmore, K.On Turan's lemma. Bull. London Math. Soc. 3 (1971), 313–317.Google Scholar