Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Crossley, M.
1999.
Monomial Bases for 𝐻*(𝐂𝐏^{∞}×𝐂𝐏^{∞}) over 𝒜(𝓅).
Transactions of the American Mathematical Society,
Vol. 351,
Issue. 1,
p.
171.
Pengelley, David
and
Williams, Frank
2011.
A new action of the Kudo–Araki–May algebra on the dual of the symmetric algebras, with applications to the hit problem.
Algebraic & Geometric Topology,
Vol. 11,
Issue. 3,
p.
1767.
Pengelley, David
and
Williams, Frank
2013.
The hit problem forH∗(BU(2); 𝔽p).
Algebraic & Geometric Topology,
Vol. 13,
Issue. 4,
p.
2061.
PENGELLEY, DAVID
and
WILLIAMS, FRANK
2015.
Sparseness for the symmetric hit problem at all primes.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 158,
Issue. 2,
p.
269.
Chơn, Phan Hoàng
and
Như, Phạm Bích
2020.
The cohomology of the Steenrod algebra and the mod p Lannes-Zarati homomorphism.
Journal of Algebra,
Vol. 556,
Issue. ,
p.
656.
Pham, Bich Nhu
and
Nguyen, Tu Thinh
2024.
The hit problem of three variables for the cohomology of the classifying space BE_(s ) as a module over the mod 3 Steenrod Algebra at some low degrees .
CTU Journal of Innovation and Sustainable Development ,
Vol. 16,
Issue. 1,


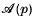 -annihilated elements in H
-annihilated elements in H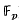 ) annihilated by the Steenrod algebra,
) annihilated by the Steenrod algebra, 