Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T22:30:07.630Z Has data issue: false hasContentIssue false
  • English
  • Français

An evaluation of the Jones polynomial of a parallel link

Published online by Cambridge University Press:  24 October 2008

Makoto Sakuma
Makoto Sakuma
Affiliation:
College of General Education, Osaka University, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

The Jones polynomial VL(t) of a link L in S3 contains certain information on the homology of the 2-fold branched covering D(L) of S3 branched along L. The following formulae are proved by Jones[3] and Lickorish and Millett[6] respectively:

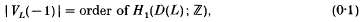
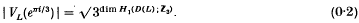
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 1 , July 1988 , pp. 105 - 113
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Brandt, R. D., Lickorish, W. B. R. and Millett, K. C.. A polynomial invariant for unoriented knots and links. Invent. Math. 84 (1986), 563–573.CrossRefGoogle Scholar
[2]Gordon, C. McA. and Litherland, R. A.. On the signature of a link. Invent. Math. 47, (1978), 53–69.CrossRefGoogle Scholar
[3]Jones, V.. A polynomial invariant for knots via von Neumann algebras. Bull. Amer. Math. Soc. 12 (1985), 103–111.CrossRefGoogle Scholar
[4]Kauffman, L. H.. State models and the Jones polynomial. Topology 26 (1987), 395–407.CrossRefGoogle Scholar
[5]Kauffman, L. H.. State models for knot polynomials. Preprint.Google Scholar
[6]Lickorish, W. B. R. and Millett, K. C.. Some evaluations of link polynomials. Comment, Math. Helv. 61 (1986), 349–359.Google Scholar
[7]Lickorish, W. B. R. and Millett, K. C.. The reversing result for the Jones polynomial. Pacific J. Math. 124 (1986), 173–176.CrossRefGoogle Scholar
[8]Murasugi, K.. Lecture delivered at the KOOK topology seminar in Osaka, 1986.Google Scholar
[9]Rolfsen, D.. Knots and Links. Math. Lecture Series, no. 7 (Publish or Perish, 1976).Google Scholar
[10]Sakuma, M.. Surface bundles over S 1 which are two-fold branched coverings of S 3. Math. Sem. Notes, Kobe Univ. 9 (1981), 159–180.Google Scholar