Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T22:27:27.369Z Has data issue: false hasContentIssue false
  • English
  • Français

An almost everywhere central limit theorem

Published online by Cambridge University Press:  24 October 2008

Gunnar A. Brosamler
Gunnar A. Brosamler
Affiliation:
Fachbereich Mathematik, Universität des Saarlandes, Saarbrücken, West Germany Department of Mathematics, The University of British Columbia, Vancouver, B.C., Canada
Get access Rights & Permissions [Opens in a new window]

Extract

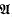The purpose of this paper is the proof of an almost everywhere version of the classical central limit theorem (CLT). As is well known, the latter states that for IID random variables Y1, Y2, … on a probability space (Ω, , P) with 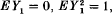we have weak convergence of the distributions of 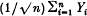to the standard normal distribution on ℝ. We recall that weak convergence of finite measures μn on a metric space S to a finite measure μ on S is defined to mean that

for all bounded, continuous real functions on S. Equivalently, one may require the validity of (1·1) only for bounded, uniformly continuous real functions, or even for all bounded measurable real functions which are μ-a.e. continuous.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 104 , Issue 3 , November 1988 , pp. 561 - 574
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Billingsley, P.. Convergence of Probability Measures (Wiley, 1968).Google Scholar
[2]Brosamler, G. A.. The asymptotic behaviour of certain additive functionals of Brownian motion. Invent. Math. 20 (1973), 87–96.CrossRefGoogle Scholar
[3]Brosamler, G. A.. Brownian occupation measures on compact manifolds. In Seminar on Stochastic Processes 1985 (Birkhäuser-Verlag, 1986), pp. 290–322.Google Scholar
[4]Brosamler, G. A.. Energy of diffusion paths and the spectrum of the Laplacian (to appear).Google Scholar
[5]Chow, Y. and Teicher, H.. Probability Theory (Springer-Verlag, 1978).CrossRefGoogle Scholar
[6]Dellacherie, C. and Meyer, P. A.. Probabilities and Potential B (North-Holland Publ. Co., 1982).Google Scholar
[7]Fisher, A.. Convex-invariant means and a pathwise central limit theorem. Adv. in Math. 63 (1987), 213–246.CrossRefGoogle Scholar
[8]Freedman, D.. Brownian Motion and Diffusion (Holden-Day, 1971).Google Scholar
[9]Reiter, H.. Classical Harmonic Analysis and Locally Compact Groups (Oxford University Press, 1968).Google Scholar